题目内容
已知数列 的前
的前 项和为
项和为 ,数列
,数列 是公比为
是公比为 的等比数列,
的等比数列, 是
是 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1)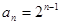 ;(2)
;(2)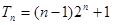 .
.
解析试题分析:(1)先根据等比数列公式求出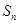 与
与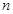 的关系式,然后利用
的关系式,然后利用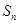 与
与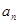 的递推关系求出
的递推关系求出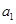 ,从而再求出
,从而再求出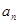 .(2)根据数列通项公式的特点用错位相减法求数列前
.(2)根据数列通项公式的特点用错位相减法求数列前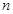 项和.
项和.
试题解析:(1)解:∵ 是公比为
是公比为 的等比数列,
的等比数列,
∴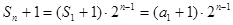 . 1分
. 1分
∴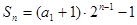 .
.
从而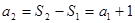 ,
,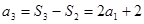 . 3分
. 3分
∵ 是
是 和
和 的等比中项
的等比中项
∴ ,解得
,解得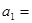
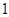 或
或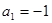 . 4分
. 4分
当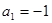 时,
时,
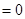 ,
, 不是等比数列, 5分
不是等比数列, 5分
∴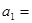
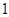 .
.
∴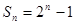 . 6分
. 6分
当 时,
时,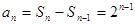 . 7分
. 7分
∵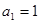 符合
符合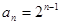 ,
,
∴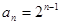 . 8分
. 8分
(2)解:∵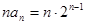 ,
,
∴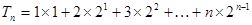 . ① 9分
. ① 9分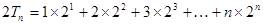 .② 10分
.② 10分
①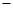 ②得
②得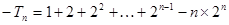 11分
11分 12分
12分 . 13分
. 13分
∴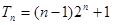 . 14分
. 14分
考点:1、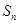 与
与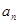 的递推关系的应用,2、错位相减法求数列前
的递推关系的应用,2、错位相减法求数列前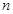 项和.
项和.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 的前n项和为
的前n项和为
 ,
,
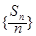 为等差数列;
为等差数列; 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn. 中,
中,
 是等比数列,并求
是等比数列,并求 ;
; 满足
满足 ,数列
,数列 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围。
的取值范围。 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.  求数列
求数列 的前
的前 项和
项和 .
. 的前
的前 项和是
项和是 ,且
,且 .
. ,求适合方程
,求适合方程 的正整数
的正整数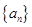 中,已知
中,已知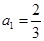 ,
,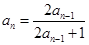 .
.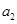 、
、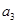 并判断
并判断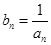 ,求证:
,求证: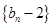 为等比数列;
为等比数列;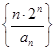 的前n项和
的前n项和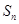 .
.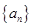 的前
的前 项和为
项和为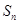 ,点
,点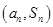 在直线
在直线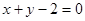 上,
上,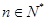 .(1)证明数列
.(1)证明数列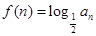 ,记
,记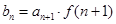 ,求数列
,求数列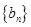 的前
的前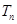 .
. ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 ;数列
;数列 为公比大于
为公比大于 的等比数列,且
的等比数列,且 为方程
为方程 的两个不相等的实根.
的两个不相等的实根. 项,第
项,第 项,第
项,第 项,……,第
项,……,第 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列 ,求数列
,求数列 项和.
项和.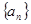 中,
中,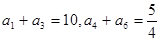 ,求其第4项及前5项和.
,求其第4项及前5项和.