Question

【题目】已知a＞0且满足不等式22a+1＞25a﹣2 ．
（1）求实数a的取值范围．
（2）求不等式loga（3x+1）＜loga（7﹣5x）．
（3）若函数y=loga（2x﹣1）在区间[1，3]有最小值为﹣2，求实数a值．

Answer 1

【答案】
（1）解：∵22a+1＞25a﹣2．

∴2a+1＞5a﹣2，即3a＜3，

∴a＜1

（2）解：∵a＞0，a＜1，∴0＜a＜1，

∵loga（3x+1）＜loga（7﹣5x）．

∴等价为 ，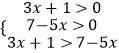

即 ，

∴ ，

即不等式的解集为（ ， ）

（3）解：∵0＜a＜1，

∴函数y=loga（2x﹣1）在区间[1，3]上为减函数，

∴当x=3时，y有最小值为﹣2，

即loga5=﹣2，

∴a﹣2= =5，

解得a=

【解析】（1）根据指数函数的单调性解不等式即可求实数a的取值范围．（2）根据对数函数的单调性求不等式loga（3x+1）＜loga（7﹣5x）．（3）根据复合函数的单调性以及对数的性质即可求出a的值．