题目内容
【题目】设函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
, ![]() 的值;
的值;
(2)当![]() 时,若存在
时,若存在![]() ,
, ![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的最小值.
的最小值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)先依据题设运用导数的几何意义建立方程求解;(2)先不等式进行等价转化与化归,再够 造函数运用导数知识分析求解:
(1)由已知得![]() ,
, ![]() ,
,  ,
,
则![]() ,且
,且![]() ,解之得
,解之得![]() ,
, ![]() .
.
(2)当![]() 时,
时, 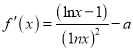 .
.
又
![]() =
= ![]() .
.
故当![]() ,即
,即![]() 时,
时, ![]() .
.
“存在![]() ,
, ![]() 使
使![]() 成立”等价于“当
成立”等价于“当![]() 时,有
时,有![]() ”,
”,
又当![]() 时,
时, ![]() ,
, ![]() ,
,
问题等价于“当![]() 时,有
时,有![]() ”.
”.
当![]() 时,
时, ![]() 在
在![]() 上为减函数,则
上为减函数,则![]()
![]() .
.
故![]() ;
;
②当![]() 时,
时, ![]()
![]() 在
在![]() 上的值域为
上的值域为![]() .
.
(i)当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上为增函数,
上为增函数,
于是![]()
![]() ,不合题意;
,不合题意;
(ii)当![]() ,即
,即![]() 时,由
时,由![]() 的单调性和值域知.
的单调性和值域知.
存在唯一![]() ,使
,使![]() ,且满足
,且满足
当![]() 时,
时, ![]() ,
, ![]() 为减函数;
为减函数;
当![]() 时,
时, ![]() ,
, ![]() 为增函数.
为增函数.
所以![]()
![]() ,
, ![]() .
.
所以![]()
![]() ,与
,与![]() 矛盾.
矛盾.
综上,得![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目