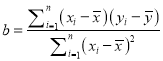题目内容
【题目】已知函数f(x)=log2(2x﹣1).
(1)求f(x)的定义域;
(2)判断函数f(x)的单调性,并用定义证明.
【答案】
(1)
解:要使函数 ![]() 的解析式有意义
的解析式有意义
自变量必须满足2x﹣1>0
即2x>1=20
∴x>0,
即f(x)的定义域为{x|x>0}
(2)
解:f(x)的在定义域内为增函数.理由如下:
设x1,x2∈(0,+∞)且x1<x2,
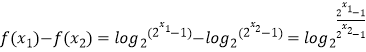 ∵x2>x1>0
∵x2>x1>0
∴ ![]()
∴ ![]()
∴ ![]()
f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
即函数f(x)为定义域内增函数
【解析】(1)根据使函数的解析式有意义的原则,结合对数函数的真数部分必须大于0,可以构造关于x的不等式,可得函数的定义域;(2)取x1 , x2∈(0,+∞)且x1<x2 , 根据对数的运算性质及指数函数的性质,判断出f(x1),f(x2)的大小,结合函数单调性的定义可得函数的单调性.
【考点精析】解答此题的关键在于理解对数函数的定义域的相关知识,掌握对数函数的定义域范围:(0,+∞),以及对对数函数的单调区间的理解,了解a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】某校从高一年级随机抽取了![]() 名学生第一学期的数学学期综合成绩和物理学期综合成绩.
名学生第一学期的数学学期综合成绩和物理学期综合成绩.
列表如下:
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
规定:综合成绩不低于![]() 分者为优秀,低于
分者为优秀,低于![]() 分为不优秀.
分为不优秀.
对优秀赋分![]() ,对不优秀赋分
,对不优秀赋分![]() ,从
,从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生,若用
名学生,若用![]() 表示这
表示这![]() 名学生两科赋分的和,求
名学生两科赋分的和,求![]() 的分布列和数学期望;
的分布列和数学期望;
根据这次抽查数据,列出![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为物理成绩与数学成绩有关?
的前提下认为物理成绩与数学成绩有关?
附:  ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|