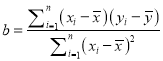题目内容
【题目】已知函数f(x)=a4x﹣a2x+1+1﹣b(a>0)在区间[1,2]上有最大值9和最小值1
(1)求a,b的值;
(2)若不等式f(x)﹣k4x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
【答案】
(1)解:令t=2x∈[2,4],
则y=at2﹣2at+1﹣b,t∈[2,4],
对称轴t=1,a>0,
∴t=2时,ymin=4a﹣4a+1﹣b=1,
t=4时,ymax=16a﹣8a+1﹣b=9,
解得a=1,b=0,
(2)解:4x﹣22x+1﹣k4x≥0在x∈[﹣1,1]上有解
设2x=t,
∵x∈[﹣1,1],
∴t∈[ ![]() ,2],
,2],
∵f(2x)﹣k.2x≥0在x∈[﹣1,1]有解,
∴t2﹣2t+1﹣kt2≥0在t∈[ ![]() ,2]有解,
,2]有解,
∴k≤ ![]() =1﹣
=1﹣ ![]() +
+ ![]() ,
,
再令 ![]() =m,则m∈[
=m,则m∈[ ![]() ,2],
,2],
∴k≤m2﹣2m+1=(m﹣1)2
令h(m)=m2﹣2m+1,
∴h(m)max=h(2)=1,
∴k≤1,
故实数k的取值范围(﹣∞,1]
【解析】(1)令t=2x∈[2,4],依题意知,y=at2﹣2at+1﹣b,t∈[2,4],由即可求得a、b的值.(2)设2x=t,k≤ ![]() =1﹣
=1﹣ ![]() +
+ ![]() ,求出函数1﹣
,求出函数1﹣ ![]() +
+ ![]() 的大值即可
的大值即可
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目