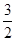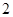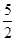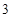题目内容
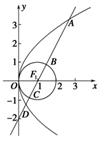
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|·|CD|的值正确的是( ).

| A.等于1 | B.最小值是1 | C.等于4 | D.最大值是4 |
A
设直线l:x=ty+1,代入抛物线方程,
得y2-4ty-4=0.设A(x1,y1),D(x2,y2),
根据抛物线定义|AF|=x1+1,|DF|=x2+1,
故|AB|=x1,|CD|=x2,所以|AB|·|CD|=x1x2=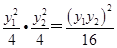 ,
,
而y1y2=-4,代入上式,得|AB|·|CD|=1.故选A.
得y2-4ty-4=0.设A(x1,y1),D(x2,y2),
根据抛物线定义|AF|=x1+1,|DF|=x2+1,
故|AB|=x1,|CD|=x2,所以|AB|·|CD|=x1x2=
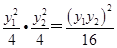 ,
,而y1y2=-4,代入上式,得|AB|·|CD|=1.故选A.

练习册系列答案
相关题目
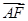 =
=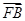 ,
,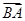 ·
·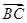 =36,则抛物线的方程为________.
=36,则抛物线的方程为________.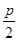 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.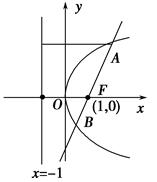
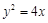 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .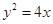 的焦点为
的焦点为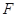 ,点
,点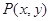 为该抛物线上的动点,又点
为该抛物线上的动点,又点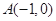 ,则
,则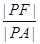 的最小值是( )
的最小值是( ) 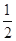

 上两点
上两点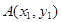 、
、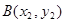 关于直线
关于直线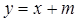 对称,且
对称,且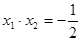 ,则
,则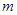 等于( )
等于( )