题目内容
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为
的距离为![]() ,以
,以![]() 为圆心且与抛物线准线
为圆心且与抛物线准线![]() 相切的圆恰好过原点
相切的圆恰好过原点![]() .点
.点![]() 是
是![]() 与
与![]() 轴的交点,
轴的交点, ![]() 两点在抛物线上且直线
两点在抛物线上且直线![]() 过
过![]() 点,过
点,过![]() 点及
点及![]() 的直线交抛物线于
的直线交抛物线于![]() 点.
点.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:直线![]() 过一定点,并求出该点坐标.
过一定点,并求出该点坐标.
【答案】(1) ![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]() ,证明见解析.
,证明见解析.
【解析】试题分析:
(1)由题意可得![]() ,则
,则![]() 为等腰三角形.过
为等腰三角形.过![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() ,据此可得抛物线的方程为
,据此可得抛物线的方程为![]() .
.
(2)设![]() 的方程为
的方程为![]() ,联立直线方程与抛物线方程可得
,联立直线方程与抛物线方程可得![]() .结合韦达定理有
.结合韦达定理有![]() .直线
.直线![]() 的方程为
的方程为![]() .可得
.可得![]() ,则直线
,则直线![]() 过定点
过定点![]() .
.
试题解析:
(1)∵![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为
的距离为![]() ,∴
,∴![]() ,
,
∵以![]() 为圆心且与抛物线准线
为圆心且与抛物线准线![]() 相切的圆恰好过原点
相切的圆恰好过原点![]() ,∴
,∴![]() ,即
,即![]() 为等腰三角形.
为等腰三角形.
过![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() ,∴
,∴![]() 得
得![]() ,
,
∴抛物线的方程为![]() .
.
(2)证明:设![]() 的方程为
的方程为![]() ,代入抛物线的方程,可得
,代入抛物线的方程,可得![]() .
.
设![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,
,
直线![]() 的方程为
的方程为![]() ,∴
,∴![]() ,
,
可得![]() ,∴
,∴![]() ,
,
∴![]() .①
.①
直线![]() 的方程为
的方程为![]() .
.
可得![]() ,②
,②
由①②可得![]() ,
, ![]() ,∴直线
,∴直线![]() 过定点
过定点![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制,已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
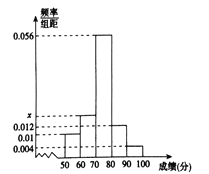
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若该校高三学生共1000人,求竞赛等级在良好及良好以上的人数;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取2名学生进行学习经验介绍,求抽取的2名学生中优秀等级的学生恰好有1人的概率.
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |
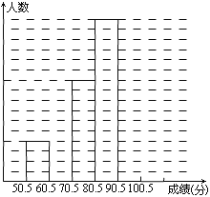
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?