题目内容
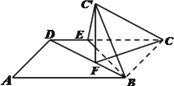
【题目】如图，长方体
中，
，
，点E是线段AB中点．
证明：
；
求二面角
的大小的余弦值；
求A点到平面
的距离．
【答案】（1）详见解析 （2）
（3）
【解析】
试题（1）
面
，
，
，又
，
[来所以，
面
所以，
（2）
是所求二面角
的平面角，
，
，二面角的大小的余弦值为（3）由（１）（２）知
，平面
的法向量为
，
试题解析：（1）证明：面，
面
所以， １分
中，
，
同理：，又，
3分
所以，面4分
又
面
所以，5分
（2）解法一 由（1）证可知是所求二面角的平面角 ６分
在
中，，；
故，
8分
即二面角的大小的余弦值为9分
解法二：利用向量法
设平面的法向量为
，
由（1）得
，
且
解得：
,即
； 7分
又平面
的法向量为
，
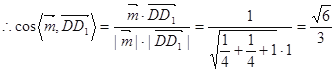
所以，二面角的余弦值为． 9分
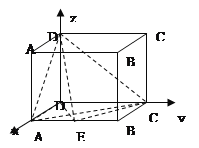
（3）解法一：
，
，
，
10分
又
，
，
，
（11分）
设
点到平面的距离为
，则
，
解得
，即点到平面的距离为． （14分）
解法二：利用向量法
由（1）（2）知，平面的法向量为
故，点到平面的距离为
练习册系列答案
相关题目
