题目内容
【题目】设f(x)=a﹣ ![]() ,x∈R,(其中a为常数).
,x∈R,(其中a为常数).
(1)若f(x)为奇函数,求a的值;
(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.
【答案】
(1)解:法一:(1因为f(x)为奇函数
所以f(﹣x)=﹣f(x)
即: ![]()
所以a=1
法二:因为x∈R,f(x)为奇函数
所以f(﹣x)=﹣f(x)
所以f(﹣0)=﹣f(0)
所以f(0)=0
得:a=1
(2)解: ![]()
因为f(x)+a>0恒成立,
即 ![]() 恒成立.
恒成立.
因为2x+1>1,
所以 ![]() .
.
所以2a≥2
即a≥1
【解析】(1)法一:利用函数的奇偶性的定义,直接求解即可.
法二:求出f(0)=0代入求解即可.(2)利用函数恒成立,分离变量,利用函数的值域求解即可.
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.

练习册系列答案
相关题目
【题目】某农科所发现,一种作物的年收获量 ![]() (单位:
(单位: ![]() )与它“相近”作物的株数
)与它“相近”作物的株数 ![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 ![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为 ![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求该作物的年收获量 ![]() 关于它“相近”作物的株数
关于它“相近”作物的株数![]() 的线性回归方程;
的线性回归方程;
(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为 ![]() ,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物 “相
,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物 “相
近”且年产量仅相差![]() 的概率.
的概率.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估
计分别为, 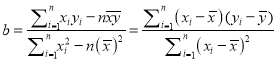 ,
, ![]()