题目内容
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1: ![]() (
(![]() ,
, ![]() ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
【答案】(1)![]() ;(2)16.
;(2)16.
【解析】试题分析:(1)根据过原点的直线的极坐标方程的定义可得![]() ,先将抛物线
,先将抛物线![]() 化为直角坐标方程,在化为极坐标方程;(2)联立直线
化为直角坐标方程,在化为极坐标方程;(2)联立直线![]() 与抛物线的方程可得
与抛物线的方程可得![]() ,同理可得
,同理可得![]() ,由
,由![]() 结合基本不等式可得结果.
结合基本不等式可得结果.
试题解析:(1)可知![]() 是过原点且倾斜角为
是过原点且倾斜角为![]() 的直线,其极坐标方程为
的直线,其极坐标方程为![]()
抛物线![]() 的普通方程为
的普通方程为![]() ,
,
其极坐标方程为![]() ,
,
化简得![]() .
.
(2)设![]() 的方程为
的方程为![]() ,由
,由![]() 得点
得点![]() ,
,
依题意得直线![]() 的方程为
的方程为![]() ,同理可得点
,同理可得点![]() ,
,
故![]()
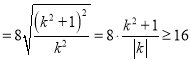 ,(当且仅当
,(当且仅当![]() 时,等号成立)
时,等号成立)
∴![]() 的面积的最小值为16.
的面积的最小值为16.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
