题目内容
已知函数f(x)= x/4+ln(x-2)/(x-4),(1)求函数f)x)的定义域和极值;(2)若函数(fx)在区间[a2-5a,8-3a]上为增函数,求实数a的取值范围;(3)函数f(x)的图象是否为中心对称图形?若是请指出对称中心,并证明;若不是,请说明理由.
解:
(1)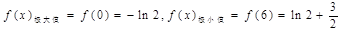 ;
;
(2)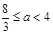 或
或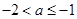 ;
;
(3)中心对称图形,对称中心是(3, 3/4).
(1)
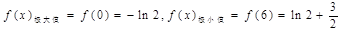 ;
;(2)
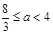 或
或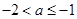 ;
;(3)中心对称图形,对称中心是(3, 3/4).
求函数f)x)的定义域 (x-2)/(x-4)
 ,
, 求极值时,令导数为0,
求极值时,令导数为0, ,得出x;若函数(fx)在区间[a2-5a,8-3a]上为增函数,则导函数在[a2-5a,8-3a]恒非负;根据函数图像,若有对称中心,则是中心一定在两极值点的中心(3, 3/4),证明时,只需证明点
,得出x;若函数(fx)在区间[a2-5a,8-3a]上为增函数,则导函数在[a2-5a,8-3a]恒非负;根据函数图像,若有对称中心,则是中心一定在两极值点的中心(3, 3/4),证明时,只需证明点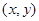
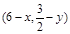 均在函数图像上。
均在函数图像上。(1)函数
 的定义域为(-∞,2)∪(4,+∞),由
的定义域为(-∞,2)∪(4,+∞),由 得:x=0或x=6,所以
得:x=0或x=6,所以 | (-∞,0) | 0 | (0,2) | (4,6) | 6 | (6,+∞) |
 | + | 0 | - | - | 0 | + |
 | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |

(2)由⑴知
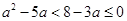 或
或 所以
所以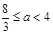 或
或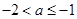
(3)由⑴知函数
 的图象若是中心对称图形,则中心一定在两极值点的中心(3, 3/4),下面证明:
的图象若是中心对称图形,则中心一定在两极值点的中心(3, 3/4),下面证明:设
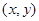 是函数
是函数 的图象上的任意一点,则
的图象上的任意一点,则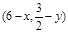 是它关于(3, 3/4)的对称点,而
是它关于(3, 3/4)的对称点,而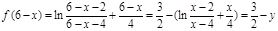 ,即
,即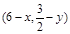 也在函数
也在函数 的图象上.所以函数
的图象上.所以函数 的图象是中心对称图形,其中心是(3, 3/4)
的图象是中心对称图形,其中心是(3, 3/4)
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

 ,其中
,其中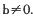
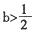 时,判断函数
时,判断函数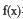 在定义域上的单调性;
在定义域上的单调性;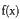 的极值点;
的极值点;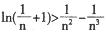 都成立.
都成立.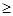 1恒成立,求a的取值集合;
1恒成立,求a的取值集合;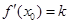 恒成立.
恒成立. (a≠0)
(a≠0) ,e]的最大值;
,e]的最大值;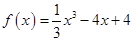 .
.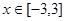 ,试求函数在此区间上的最大值与最小值.
,试求函数在此区间上的最大值与最小值.
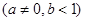 ,在区间
,在区间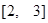 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数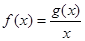 .
.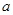 、
、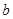 的值及函数
的值及函数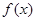 的解析式;
的解析式;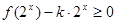 在
在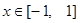 时恒成立,求实数
时恒成立,求实数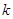 的取值范围;
的取值范围;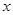 的方程
的方程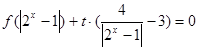 有三个相异的实数根,求实数
有三个相异的实数根,求实数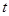 的取值范围.
的取值范围.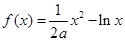 ,其中
,其中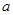 为大于零的常数.
为大于零的常数.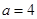 时,求函数
时,求函数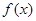 的单调区间和极值;
的单调区间和极值;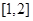 上至少存在一点
上至少存在一点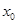 ,使得
,使得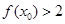 成立,求
成立,求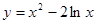 的单调增区间是( )
的单调增区间是( )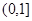 ;
;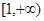 ;
; 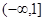 及
及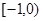 及
及