题目内容
7.函数y=${x}^{-\frac{2}{3}}$定义域是{x|x≠0},值域是{y|y>0};奇偶性:偶函数,单调区间(-∞,0),(0,+∞).分析 把函数y化为根式的形式,求出它的定义域和值域;
再根据函数奇偶性与单调性的定义进行判断,即可得出正确的结论.
解答 解:∵函数y=${x}^{-\frac{2}{3}}$=$\frac{1}{\root{3}{{x}^{2}}}$,
∴x2≠0,
解得x≠0,
∴函数y的定义域是{x|x≠0};
又y>0,
∴函数y的值域是{y|y>0};
又对定义域内的任意x,有f(-x)=$\frac{1}{\root{3}{{(-x)}^{2}}}$=$\frac{1}{\root{3}{{x}^{2}}}$=f(x),
∴y=f(x)是定义域上的偶函数;
又y=f(x)=${x}^{-\frac{2}{3}}$,
当x>0时,f(x)是减函数,
x<0时,f(x)是增函数,
∴(-∞,0)和(0,+∞)是函数的单调区间.
故答案为:{x|x≠0};{y|y>0};偶函数;(-∞,0),(0,+∞).
点评 本题考查了求函数的定义域和值域的应用问题,也考查了函数奇偶性与单调性的判断问题,是基础题目.

练习册系列答案
相关题目
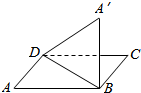 如图,在边长为2的菱形ABCD中,∠BAD=60°,现将△ABD沿BD翻折至△A′BD,使二面角A′-BD-C的大小为60°,求CD和平面A′BD所成角的余弦值是$\frac{{\sqrt{7}}}{4}$.
如图,在边长为2的菱形ABCD中,∠BAD=60°,现将△ABD沿BD翻折至△A′BD,使二面角A′-BD-C的大小为60°,求CD和平面A′BD所成角的余弦值是$\frac{{\sqrt{7}}}{4}$.