题目内容
16.已知数列{an}满足a1=$\frac{2}{3}$,an+1=$\frac{{a}_{n}-2}{2{a}_{n}-3}$(n∈N*).(1)求证:{$\frac{1}{{a}_{n}-1}$}是等差数列,并求出{an}的通项an;
(2)证明:对于n∈N*,a1•a2•a3•…•an$<\frac{1}{\sqrt{n+1}}$.
分析 (1)在原递推式的两边同时减1,取倒数,结合等差数列的定义和通项公式,即可得到;
(2)由于$\frac{2n}{2n+1}$<$\frac{2n+1}{2n+2}$,令S=a1•a2•a3•…•an=$\frac{2}{3}$•$\frac{4}{5}$•$\frac{6}{7}$…$\frac{2n}{2n+1}$<$\frac{3}{4}$•$\frac{5}{6}$•$\frac{7}{8}$…$\frac{2n+1}{2n+2}$,两边乘以S,即可得证.
解答 证明:(1)由a1=$\frac{2}{3}$,an+1=$\frac{{a}_{n}-2}{2{a}_{n}-3}$(n∈N*).
可得an+1-1=$\frac{{a}_{n}-2}{2{a}_{n}-3}$-1=$\frac{1-{a}_{n}}{2{a}_{n}-3}$,
即有$\frac{1}{{a}_{n+1}-1}$=$\frac{1}{{a}_{n}-1}$-2,
则有{$\frac{1}{{a}_{n}-1}$}是首项为-3,公差为2的等差数列,
即有$\frac{1}{{a}_{n}-1}$=-3-2(n-1),
化简可得an=$\frac{2n}{2n+1}$;
(2)令S=a1•a2•a3•…•an=$\frac{2}{3}$•$\frac{4}{5}$•$\frac{6}{7}$…$\frac{2n}{2n+1}$,
由于$\frac{2n}{2n+1}$<$\frac{2n+1}{2n+2}$,
则S<$\frac{3}{4}$•$\frac{5}{6}$•$\frac{7}{8}$…$\frac{2n+1}{2n+2}$,
即有S2<$\frac{2}{3}$•$\frac{3}{4}$•$\frac{4}{5}$•$\frac{5}{6}$…$\frac{2n}{2n+1}$•$\frac{2n+1}{2n+2}$
=$\frac{2}{2n+2}$=$\frac{1}{n+1}$,
即为S<$\frac{1}{\sqrt{n+1}}$.
则原不等式成立.
点评 本题考查等差数列的定义和通项公式的运用,考查不等式的证明,注意运用真分数的特点:分子分母同时加一个正数,分数值增加,属于中档题.

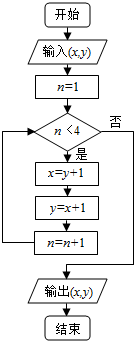
| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |