题目内容
已知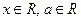 ,
,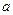 为常数,且
为常数,且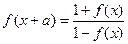 ,则函数
,则函数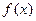 必有一周期为: ( )
必有一周期为: ( )
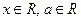 ,
,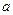 为常数,且
为常数,且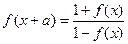 ,则函数
,则函数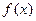 必有一周期为: ( )
必有一周期为: ( )A.2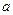 | B.3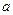 | C.4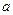 | D.5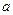 |
C
由于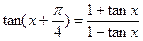 ,从而函数
,从而函数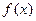 的一个背景为正切函数tanx,取
的一个背景为正切函数tanx,取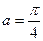 ,可得必有一周期为4
,可得必有一周期为4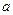 。故选C。
。故选C。
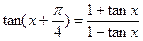 ,从而函数
,从而函数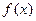 的一个背景为正切函数tanx,取
的一个背景为正切函数tanx,取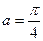 ,可得必有一周期为4
,可得必有一周期为4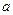 。故选C。
。故选C。
练习册系列答案
相关题目
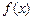 在
在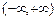 上满足
上满足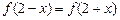 ,
, 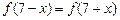 且在闭区间[0, 7]上只有
且在闭区间[0, 7]上只有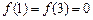 .
. 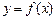 的奇偶性;
的奇偶性;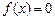 在闭区间
在闭区间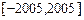 上的根的个数, 并证明你的结论.
上的根的个数, 并证明你的结论.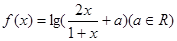 是奇函数,则a= .
是奇函数,则a= .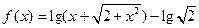
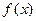 的奇偶性。 (2)判断函数
的奇偶性。 (2)判断函数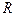 上的奇函数
上的奇函数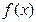 满足
满足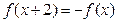 ,则
,则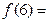
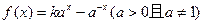
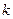 的值;
的值;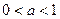 ,
,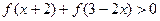 ,求
,求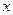 的取值范围;
的取值范围;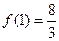 ,且函数
,且函数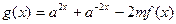 在
在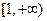 上的最小值为
上的最小值为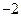 ,求
,求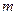 的值
的值 ,
, 的奇偶性; ⑵证明
的奇偶性; ⑵证明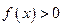 .
.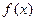 是
是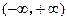 上的奇函数,
上的奇函数,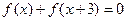 ,当
,当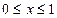 时,
时,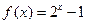 ,则
,则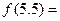 。
。 是R上的奇函数,且
是R上的奇函数,且 ,则
,则