题目内容
设函数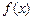 在
在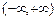 上满足
上满足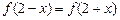 ,
, 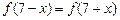 且在闭区间[0, 7]上只有
且在闭区间[0, 7]上只有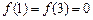 .
.
⑴试判断函数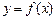 的奇偶性;
的奇偶性;
⑵试求方程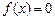 在闭区间
在闭区间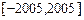 上的根的个数, 并证明你的结论.
上的根的个数, 并证明你的结论.
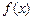 在
在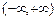 上满足
上满足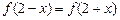 ,
, 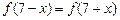 且在闭区间[0, 7]上只有
且在闭区间[0, 7]上只有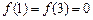 .
. ⑴试判断函数
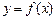 的奇偶性;
的奇偶性;⑵试求方程
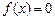 在闭区间
在闭区间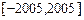 上的根的个数, 并证明你的结论.
上的根的个数, 并证明你的结论.(1)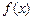 为非奇非偶函数(2)方程
为非奇非偶函数(2)方程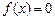 在
在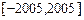 上共有802个根
上共有802个根
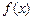 为非奇非偶函数(2)方程
为非奇非偶函数(2)方程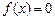 在
在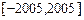 上共有802个根
上共有802个根⑴由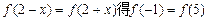
∵在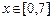 上只有
上只有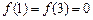
∴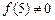 ∴
∴
故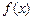 为非奇非偶函数。
为非奇非偶函数。
⑵由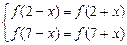 得
得 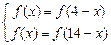

∴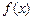 是以10为周期的函数. 又
是以10为周期的函数. 又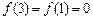
∴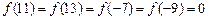
∴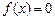 在[0, 10]和
在[0, 10]和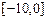 上各有2个根.
上各有2个根.
从而方程在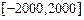 上有800个根, 而
上有800个根, 而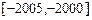 上没有根,
上没有根,
在[2000, 2005]上有2个根.
故方程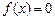 在
在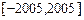 上共有802个根.
上共有802个根.
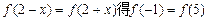
∵在
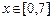 上只有
上只有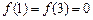
∴
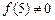 ∴
∴
故
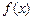 为非奇非偶函数。
为非奇非偶函数。 ⑵由
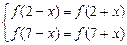 得
得 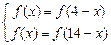

∴
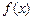 是以10为周期的函数. 又
是以10为周期的函数. 又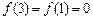
∴
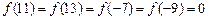
∴
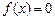 在[0, 10]和
在[0, 10]和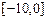 上各有2个根.
上各有2个根. 从而方程在
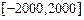 上有800个根, 而
上有800个根, 而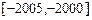 上没有根,
上没有根, 在[2000, 2005]上有2个根.
故方程
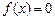 在
在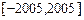 上共有802个根.
上共有802个根. 
练习册系列答案
相关题目
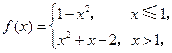 则
则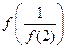 的值为( )
的值为( )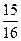
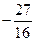
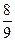
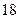
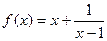 ,证明:函数
,证明:函数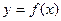 的图象是一个中心对称图形,并求其对称中心
的图象是一个中心对称图形,并求其对称中心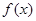 ,若
,若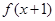 都是偶函数,则( )
都是偶函数,则( )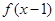 是奇函数
是奇函数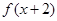 是偶函数
是偶函数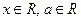 ,
,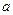 为常数,且
为常数,且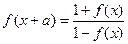 ,则函数
,则函数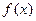 必有一周期为: ( )
必有一周期为: ( )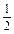 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.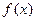 满足
满足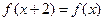 ,且当
,且当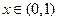 时,
时,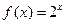 ,则
,则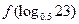 的值等于
的值等于 
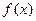 在区间[0,
在区间[0,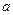 ](
](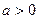 )上是单调函数,且
)上是单调函数,且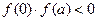 ,则方程
,则方程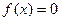 在区间[-
在区间[-