题目内容
文科(本小题满分14分)设函数 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数m的取值范围。)
都成立,求实数m的取值范围。)
(1),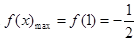 ;(2)
;(2)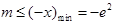 。
。
解析试题分析:(1)①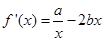
 函数
函数 在
在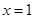 处与直线
处与直线 相切
相切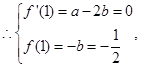 解得
解得 3分
3分
②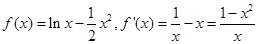
当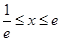 时,令
时,令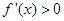 得
得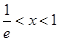 ;令
;令 ,得
,得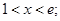
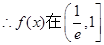 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,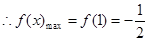 8分
8分
(2)当b=0时,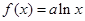 若不等式
若不等式 对所有的
对所有的 都成立,
都成立,
则 对所有的
对所有的 都成立,
都成立,
即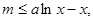 对所有的
对所有的 都成立,
都成立,
令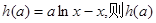 为一次函数,
为一次函数,
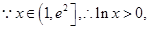
 上单调递增
上单调递增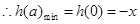 ,
,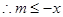 对所有的
对所有的 都成立
都成立
 14分
14分
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性、最值及不等式恒成立问题。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。通过研究函数的单调区间、最值情况,得到使不等式还差了点条件。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,直线x+y=3以及两坐标轴所围成的图形的面积S.
,直线x+y=3以及两坐标轴所围成的图形的面积S.
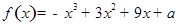 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值.
上的最大值和最小值.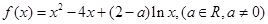
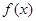 的单调区间;
的单调区间;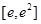 上的最小值.
上的最小值. ,
, .求函数
.求函数 的单调递减区间;
的单调递减区间; 在
在 上是增函数.
上是增函数.
 的解析式及减区间;
的解析式及减区间; 的最小值。
的最小值。
 在点
在点 处的切线与直线
处的切线与直线 垂直,求a的值;
垂直,求a的值;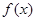 的单调区间;
的单调区间;