题目内容
已知函数
(1)若函数 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(2)当 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.
(1) (2)
(2) ,
,
解析试题分析:(1)由已知得 , 1分
, 1分
依题意得 对任意
对任意 恒成立
恒成立
即 对任意
对任意 恒成立, 3分
恒成立, 3分
而 4分
4分
所以 的取值范围为
的取值范围为 5分
5分
(2)当 时,
时, , 6分
, 6分
令 ,得
,得 , 7分
, 7分
若 时,
时, ,若
,若 时,
时, ,
,
故 是函数在区间
是函数在区间 上的唯一的极小值,也是最小值,
上的唯一的极小值,也是最小值,
即 ,而
,而 , 10分
, 10分
由于 , 12分
, 12分
则 14分
14分
考点:本小题主要考查利用导数求函数的单调性,极值,最值等,以及恒成立问题的解决.
点评:利用导数研究函数的性质时,要注意步骤完整,最好列表格进行说明单调性、极值、最值等,而且要注意函数的定义域.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 若存在函数
若存在函数 使得
使得 恒成立,则称
恒成立,则称 的一个“下界函数”.
的一个“下界函数”. 为实数
为实数 为
为 的取值范围;
的取值范围; 试问函数
试问函数 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由. ,其中
,其中 。
。 有极值
有极值 ,求
,求 的值;
的值; 在区间
在区间 上为增函数,求
上为增函数,求
 .
. 的单调区间;
的单调区间; ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在点
在点 处的切线与x轴交点的横坐标为an.
处的切线与x轴交点的横坐标为an. ,求数到
,求数到 的前n项和Sn.
的前n项和Sn. 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数m的取值范围。)
都成立,求实数m的取值范围。) ,
, 所围成的封闭图形的面积
所围成的封闭图形的面积 在区间
在区间 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求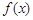 的解析式.
的解析式.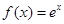 ,其图像在点
,其图像在点 处的切线为
处的切线为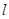 .
. 、直线
、直线 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积; 轴围成图形的面积.
轴围成图形的面积.