题目内容
9.已知数列{an}是公差d>0的等差数列,其中a1、a2是方程x2-3x+2=0的两根.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记${b_n}={2^{a_n}}+{(-1)^n}{a_n}$,求数列{bn}的前100项和T100.
分析 (Ⅰ)由x2-3x+2=0,解得x.可得a1,a2,利用等差数列的通项公式即可得出;
(Ⅱ)由${b_n}={2^{a_n}}+{(-1)^n}{a_n}={2^n}+{(-1)^n}n$,利用等比数列的前n项和公式即可得出.
解答 解:(Ⅰ)∵x2-3x+2=0,解得x=1,或x=2.
由题意得a1=1,a2=2,
∴d=1,
∴an=1+(n-1)•1=n.
(Ⅱ)∵${b_n}={2^{a_n}}+{(-1)^n}{a_n}={2^n}+{(-1)^n}n$,
∴${T_{100}}=\frac{{2(1-{2^{100}})}}{1-2}+[(-1+2)+(-3+4)+…+(-99+100)]$
=2101-2+50=2101+48.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、分组求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.如果点M(sinθ,cosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
17.复数$z=3i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.直线2x-y+1=0关于y轴对称的直线方程是( )
| A. | 2x+y-1=0 | B. | 2x+y+1=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
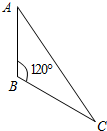 在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,
在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,