题目内容
4.已知曲线Γ为函数f(x)=3x-x3的图象,过点A(2,2)作曲线Γ的切线,可能的切线条数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 设出切点P(m,3m-m3),利用导数求出过切点的切线方程,代入M点坐标,然后再利用导数求解关于m的方程的解的个数,则答案可求.
解答 解:设切点为P(m,3m-m3),
由f(x)=3x-x3,得f′(x)=3-3x2,
∴切线的斜率k=3-3m2,
得曲线过P点的切线方程为y-3m+m3=(3-3m2)(x-m),
即y=3(1-m2)x+2m3,
∵切线过点M(2,2),
故2=6-6m2+2m3,
即2m3-6m2+4=0,
令h(m)=2m3-6m2+4,
则h′(m)=6m2-12m,
由h′(m)=0,解得m=0或m=2,
当m∈(-∞,0),(2,+∞)时,h′(m)>0,
当m∈(0,2)时,h′(m)<0.
∴h(m)的极大值、极小值分别为h(0)=5>0,
h(2)=-3<0,
故其图象与x轴交点3个,
也就是切线条数为3.
故选:A.
点评 本题考查利用导数研究曲线上某点处的切线方程,考查了函数零点个数的判断,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
14.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-1),则向量$\frac{1}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$=( )
| A. | (-2,-1) | B. | (-2,1) | C. | (-1,0) | D. | (-1,2) |
15.设△ABC的内角A、B、C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
19.抛物线x2=2y的焦点到准线的距离是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
16.如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,E为线段CD上一动点,现将△AED沿AE折起,使平面AED⊥平面ABC,当E从D运动到C,则D在平面ABC上的射影K所形成轨迹的长度为( )
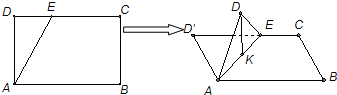

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
13.sin75°=( )
| A. | $\frac{\sqrt{6}-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |