题目内容
若定义在R上的偶函数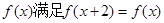 ,且当
,且当 则函数
则函数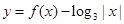 的零点个数是 ( )
的零点个数是 ( )
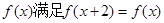 ,且当
,且当 则函数
则函数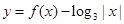 的零点个数是 ( )
的零点个数是 ( )| A.多于4个 | B.4个 | C.3个 | D.2个 |
B
分析:根据定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,我们易画出函数f(x)的图象,然后根据函数y=f(x)-log3|x|的零点个数,即为对应方程的根的个数,即为函数y=f(x)与函数y=log3|x|的图象交点的个数,利用图象法得到答案.
解答:解:若函数f(x)满足f(x+2)=f(x),
则函数是以2为周期的周期函数,
又由函数是定义在R上的偶函数,
结合当x∈[0,1]时,f(x)=x,
我们可以在同一坐标系中画出函数y=f(x)与函数y=log3|x|的图象如下图所示:
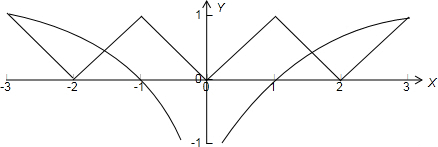
由图可知函数y=f(x)与函数y=log3|x|的图象共有4个交点,
即函数y=f(x)-log3|x|的零点个数是4个,
故选B
解答:解:若函数f(x)满足f(x+2)=f(x),
则函数是以2为周期的周期函数,
又由函数是定义在R上的偶函数,
结合当x∈[0,1]时,f(x)=x,
我们可以在同一坐标系中画出函数y=f(x)与函数y=log3|x|的图象如下图所示:

由图可知函数y=f(x)与函数y=log3|x|的图象共有4个交点,
即函数y=f(x)-log3|x|的零点个数是4个,
故选B

练习册系列答案
相关题目
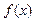 在其定义域上满足
在其定义域上满足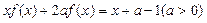 .
.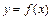 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);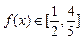 时,求x的取值范围;
时,求x的取值范围;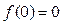 ,数列
,数列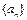 满足
满足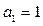 ,那么:
,那么: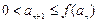 ,正整数N满足
,正整数N满足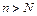 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列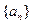 ,
,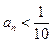 恒成立,求最小的N;
恒成立,求最小的N;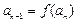 ,求证:
,求证: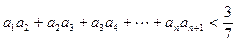 .
.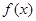 是定义在
是定义在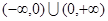 上的偶函数,当
上的偶函数,当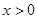 时,
时,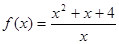
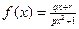 有最大值
有最大值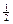 , 且
, 且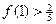 , 其中实数
, 其中实数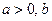 是正整数.
是正整数.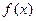 的解析式;
的解析式;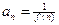 , 证明
, 证明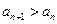 (
(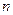 是正整数).
是正整数).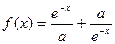 是定义在R上的函数
是定义在R上的函数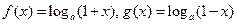 其中
其中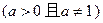 ,
,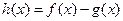 .
.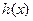 的定义域,判断
的定义域,判断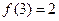 ,求使
,求使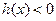 成立的
成立的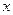 的集合
的集合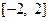 上的偶函数
上的偶函数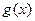 ,当
,当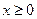 时
时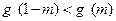 , 则实数
, 则实数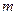 的取值范围是 ▲ .
的取值范围是 ▲ .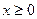 时,
时,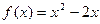 ,则f(x)在R上的表达式是( )
,则f(x)在R上的表达式是( )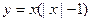
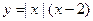
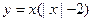
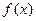 是定义在R上的奇函数,若
是定义在R上的奇函数,若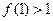 ,
, 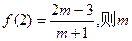 的取值范围是 .
的取值范围是 .