题目内容
(本小题满分12分)
已知函数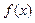 在其定义域上满足
在其定义域上满足 .
.
(1)函数 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当 时,求x的取值范围;
时,求x的取值范围;
(3)若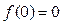 ,数列
,数列 满足
满足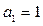 ,那么:
,那么:
①若 ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
, 恒成立,求最小的N;
恒成立,求最小的N;
②若 ,求证:
,求证: .
.
已知函数
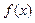 在其定义域上满足
在其定义域上满足 .
.(1)函数
 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);(2)当
 时,求x的取值范围;
时,求x的取值范围;(3)若
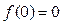 ,数列
,数列 满足
满足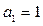 ,那么:
,那么:①若
 ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
, 恒成立,求最小的N;
恒成立,求最小的N;②若
 ,求证:
,求证: .
.解:(1)依题意有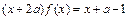 .若
.若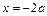 ,则
,则 ,得
,得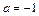 ,这与
,这与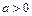 矛盾,∴
矛盾,∴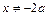 ,∴
,∴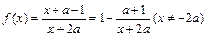 ,故
,故 的图象是中心对称图形,其对称中心为点
的图象是中心对称图形,其对称中心为点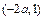 .………(3分)
.………(3分)
(2)∵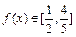 ,∴
,∴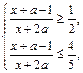 即
即 又∵
又∵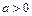 ,∴
,∴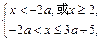
得 .………(6分)
.………(6分)
(3)①由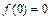 得
得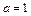 ,∴
,∴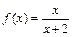 .由
.由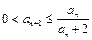 得
得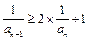 ,
,
即 .令
.令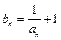 ,则
,则 ,又∵
,又∵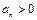 ,∴
,∴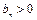 ,∴
,∴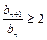 .
.
∵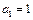 ,∴
,∴ ,∴当
,∴当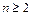 时,
时,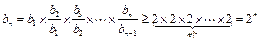 .
.
【或∵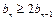 ,∴
,∴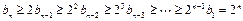 】
】
又∵ 也符合
也符合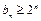 ,∴
,∴ ,即
,即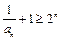 ,得
,得 .要使
.要使 恒成立,只需
恒成立,只需 ,即
,即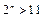 ,∴
,∴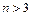 .故满足题设要求的最小正整数
.故满足题设要求的最小正整数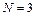
② 由①知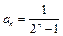 ,∴
,∴ ,
,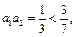

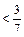 ,∴当
,∴当 时,不等式成立.
时,不等式成立.
证法1:∵ ,∴当
,∴当 时,
时,



 .………(12分)
.………(12分)
证法2:∵ ,∴当
,∴当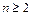 时,
时,
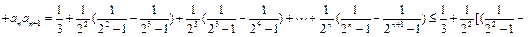
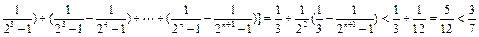 .………(12分)
.………(12分)
证法3:∵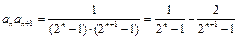 ,∴当
,∴当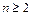 时,
时,
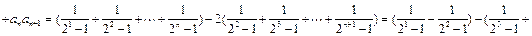
 (12分)
(12分)
证法4:当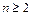 时,∵
时,∵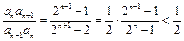 ,∴
,∴
 ,∴
,∴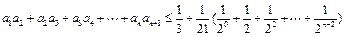
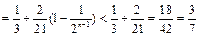 .………(12分)
.………(12分)
证法5:∵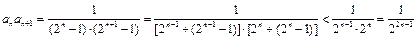 ,
,
∴当 时,
时,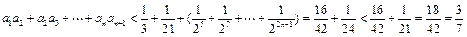 .
.
综上,对任意的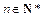 ,都有
,都有 .………(12分)
.………(12分)
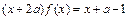 .若
.若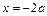 ,则
,则 ,得
,得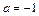 ,这与
,这与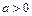 矛盾,∴
矛盾,∴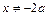 ,∴
,∴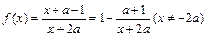 ,故
,故 的图象是中心对称图形,其对称中心为点
的图象是中心对称图形,其对称中心为点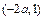 .………(3分)
.………(3分)(2)∵
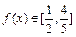 ,∴
,∴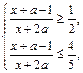 即
即 又∵
又∵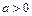 ,∴
,∴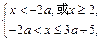
得
 .………(6分)
.………(6分)(3)①由
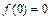 得
得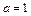 ,∴
,∴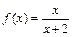 .由
.由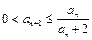 得
得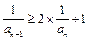 ,
,即
 .令
.令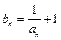 ,则
,则 ,又∵
,又∵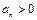 ,∴
,∴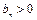 ,∴
,∴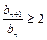 .
.∵
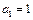 ,∴
,∴ ,∴当
,∴当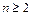 时,
时,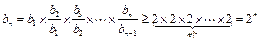 .
.【或∵
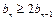 ,∴
,∴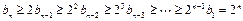 】
】又∵
 也符合
也符合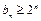 ,∴
,∴ ,即
,即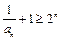 ,得
,得 .要使
.要使 恒成立,只需
恒成立,只需 ,即
,即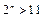 ,∴
,∴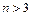 .故满足题设要求的最小正整数
.故满足题设要求的最小正整数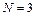
② 由①知
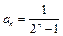 ,∴
,∴ ,
,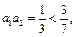

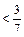 ,∴当
,∴当 时,不等式成立.
时,不等式成立.证法1:∵
 ,∴当
,∴当 时,
时,



 .………(12分)
.………(12分)证法2:∵
 ,∴当
,∴当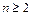 时,
时,
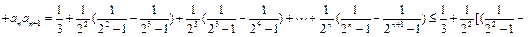
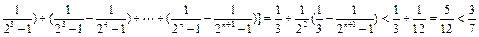 .………(12分)
.………(12分)证法3:∵
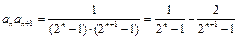 ,∴当
,∴当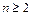 时,
时,
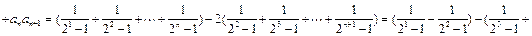
 (12分)
(12分)证法4:当
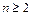 时,∵
时,∵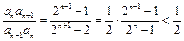 ,∴
,∴
 ,∴
,∴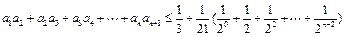
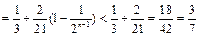 .………(12分)
.………(12分)证法5:∵
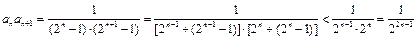 ,
,∴当
 时,
时,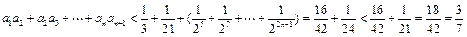 .
.综上,对任意的
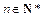 ,都有
,都有 .………(12分)
.………(12分)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
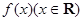 为奇函数,
为奇函数,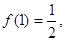
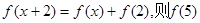 = ( )
= ( )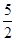
 ,且当
,且当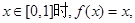 则函数
则函数 的零点个数是 ( )
的零点个数是 ( )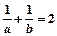 ,则A=____
,则A=____ ____。
____。 为奇函数,则
为奇函数,则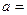 ______.
______.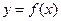 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时,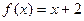 ,那么不等式
,那么不等式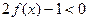 的解集是( )
的解集是( )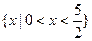
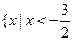 或
或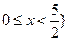
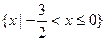
 或
或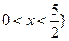
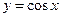 ,
,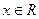
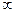 )上是减函数,如果
)上是减函数,如果 且| x1 | < | x2 | , 则有( )
且| x1 | < | x2 | , 则有( )