题目内容
(本小题满分14分)
已知奇函数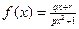
有最大值
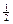, 且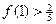
, 其中实数
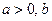是正整数.
求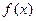
的解析式;
令
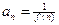, 证明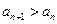
(
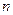是正整数).
已知奇函数
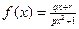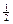有最大值, 且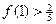, 其中实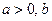数是正整数.求
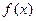的解析式;令
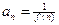, 证明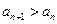(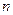是正整数).（1）
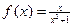
（2）证明略
(1) 由奇函数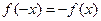
可得
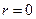, --- 2分
x > 0时，由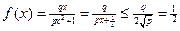
① 以及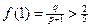
② --- 4分
可得到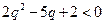
, 
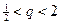, 只有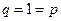
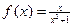, ∴; --- 2分
(2)
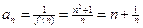, --- 2分
则由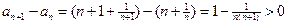
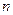(是正整数),
可得所求证结论. --- 4分
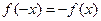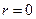可得, --- 2分x > 0时，由
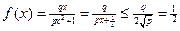① 以及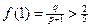② --- 4分可得到
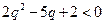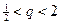, , 只有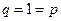, ∴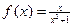; --- 2分(2)
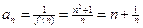, --- 2分则由
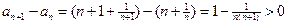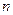(是正整数),可得所求证结论. --- 4分
练习册系列答案
相关题目
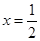
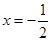
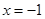
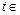R，m，n都是不为1的正数，函数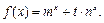
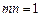，请判断函数
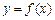是否具有奇偶性. 如果具有，求出相
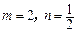，且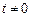
，请判断函数
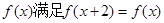，且当
则函数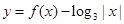
的零点个数是 （ ）
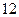分）
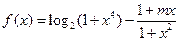
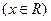是偶函数.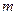
的值，并给出函数
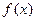的单调区间（不要求证明）；
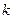为实常数，解关于
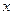的不等式：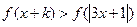
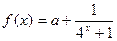是奇函数．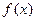
的单调性（不必说明单调性理由）；
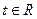，不等式
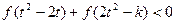恒成立，求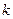
的取值范围．
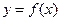是定义在R上的奇函数，当
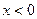时，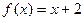
，那么不等式
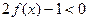的解集是( )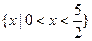
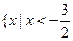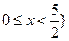
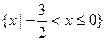
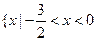或
或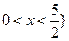
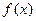是定义在R上的奇函数，并且当
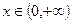时，
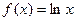，那么，
. 
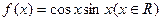，给出下列四个命题：
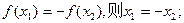②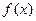
的最小正周期是
；
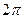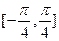上是增函数； ④
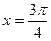对称；
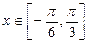时，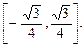
其中正确的命题为（ ）