题目内容
【题目】现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P﹣A1B1C1D1 ， 下部的形状是正四棱柱ABCD﹣A1B1C1D1（如图所示），并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．
（1）若AB=6m，PO1=2m,则仓库的容积是多少？
（2）若正四棱柱的侧棱长为6m,则当PO1为多少时，仓库的容积最大？
【答案】
（1）
解： 
，则 
，
， 
，
，
故仓库的容积为 
（2）
解：设 
，仓库的容积为 
则 
， 
， 
，
，
，
，
，
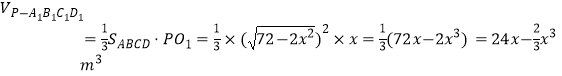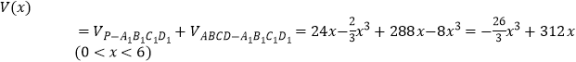当 
时， 
， 单调递增，
当 
时， 
， 单调递减，
因此，当 
时， 取到最大值，
即 
时，仓库的容积最大
【解析】（1）由正四棱柱的高O1O是正四棱锥的高PO1的4倍，可得PO1=2m时，O1O=8m，进而可得仓库的容积；（2）设PO1=xm，则O1O=4xm，A1O1= 
m，A1B1= m，代入体积公式，求出容积的表达式，利用导数法，可得最大值
练习册系列答案
阅读快车系列答案
相关题目
