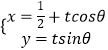Question

【题目】椭圆 经过 为坐标原点，线段 的中点在圆 上.
（1）求 的方程；
（2）直线 不过曲线 的右焦点 ，与 交于 两点，且 与圆 相切，切点在第一象限， 的周长是否为定值？并说明理由.

Answer 1

【答案】
（1）解：由题意得 ，
由题意得， 的中点 在圆 上，
所以 ，得 ，
所以椭圆方程为
（2）解：依题意可设直线 ，
因为直线 与圆 相切，且切点的第一象限，
所以 ，且有 ，
设 ，将直线 与椭圆方程联立
可得， ， ，且
，
因为 ，故 ，
另一方面
，
化简得 ，同理 ，可得 ，
由此可得 的周长 ，
故 的周长为定值
【解析】(1)结合题意由待定数据法代入数值求出结果即可。(2)根据直线与相切切点在第一象限找出m与k的关系联立直线与椭圆的方程消元结合韦达定理找出 x1 + x2 ，x1x2的关系代入到弦长公式中，再求出另两边的长度即可求出三角形周长的代数式整理化简即可得到结果。