题目内容
【题目】设A是双曲线 ![]() 的右顶点,F(c,0)是右焦点,若抛物线
的右顶点,F(c,0)是右焦点,若抛物线 ![]() 的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
A.[2,+∞)
B.(1,2]
C.(1,3]
D.[3,+∞)
【答案】A
【解析】解:抛物线 ![]() 的准线l为x=
的准线l为x= ![]() ,
,
双曲线 ![]() 的右顶点A(a,0),
的右顶点A(a,0),
F(c,0)是右焦点,
设l与x轴的交点为H,设P( ![]() ,h),h>0,
,h),h>0,
在直角三角形PHA中,可得tan∠APH= ![]() =
= ![]() ,
,
在直角三角形PHF中,可得tan∠FPH= ![]() =
= ![]() ,
,
即有tan∠APF=tan(∠FPH﹣∠APH)
=  =
= 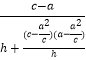 ≤
≤ ![]() ,
,
即为tan30°= ![]() ≤
≤ ![]() ,
,
化简可得3c2≥4ac+4a2,
由e= ![]() 可得3e2﹣4e﹣4≥0,
可得3e2﹣4e﹣4≥0,
解得e≥2或e≤﹣ ![]() (舍去),
(舍去),
故选:A.


练习册系列答案
相关题目