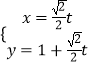题目内容
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 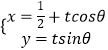 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
【答案】
(1)解:∵曲线C的极坐标方程为ρsin2α﹣2cosα=0,
∴ρ2sin2α=2ρcosα,
∴曲线C的直角坐标方程为y2=2x.
(2)直线l的参数方程 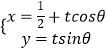 ,(t为参数,0<θ<π),
,(t为参数,0<θ<π),
把直线的参数方程化入y2=2x,得t2sin2θ﹣2tcosθ﹣1=0,
设A,B两点对应的参数分别为t1,t2,
则 ![]() ,t1t2=﹣
,t1t2=﹣ ![]() ,
,
|AB|=|t1﹣t2|= ![]()
= ![]() =
= ![]() ,
,
∴当 ![]() 时,|AB|取最小值2.
时,|AB|取最小值2.
【解析】1、本题考查的是双曲线的极坐标方程![]() ,根据题意可得。
,根据题意可得。
2、由直线的参数方程得到抛物线的方程,再转化成极坐标方程。设A,B两点对应的参数分别为t1,t2由题意可得|AB|=|t1﹣t2|![]()
∴当 θ = π 2 时,|AB|取最小值2

练习册系列答案
相关题目