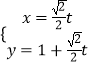Question

【题目】给出下列命题：
①x∈R，不等式x2＋2x>4x－3均成立；
②若log2x＋logx2≥2，则x>1；
③“若a>b>0且c<0，则 ”的逆否命题；
④若p且q为假命题，则p，q均为假命题．
其中真命题是( )
A.①②③
B.①②④
C.①③④
D.②③④

Answer 1

【答案】A
【解析】①中不等式可表示为(x－1)2＋2>0，恒成立；②中不等式可变为log2x＋ ≥2，得x>1；③中由a>b>0，得 ，而c<0，所以原命题是真命题，则它的逆否命题也为真；④由p且q为假只能得出p，q中至少有一个为假，④不正确．
所以答案是:A
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案，需要熟知两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．