题目内容
20.已知函数f(x)=lnx-$\frac{1}{2}$ax2+x,a∈R(1)若f(1)=0,求函数的最大值
(2)令g(x)=f(x)-(ax-1),求函数g(x)的单调区间.
分析 (1)代入f(1)=ln1-$\frac{1}{2}$a+1=0,求a值,利用导数的正负判断函数单调性,利用单调性求最值
(2)求g'(x)=$\frac{-a(x+1)(x-\frac{1}{a})}{x}$,利用二次函数知识对a进行分类讨论得出g(x)的单调区间
解答 解:(1)f(1)=ln1-$\frac{1}{2}$a+1=0,
∴a=2,
∴f(x)=lnx-x2+x,
f'(x)=$\frac{1}{x}$-2x+1
=-$\frac{(2x+1)(x-1)}{x}$,
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,
故函数f(x)的单调递增区间是(0,1);单调递减区间是(1,+∞),
∴函数的最大值为f(1)=0;
(2)g(x)=f(x)-(ax-1)
=lnx-$\frac{1}{2}$ax2+x-ax+1,
g'(x)=$\frac{-a(x+1)(x-\frac{1}{a})}{x}$,
①当a>0时,令g'(x)>0,解得0<x<$\frac{1}{a}$; 令g'(x)<0,解得x>$\frac{1}{a}$,
所以函数f(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减;
②当a<0时,
显然,在(0,+∞)上,g'(x)>0,函数f(x)在(0,+∞)上单调递增;
③当a=0时,g'(x)=$\frac{x+1}{x}$,
显然,在(0,+∞)上,g'(x)>0,函数f(x)在(0,+∞)上单调递增.
点评 考察了导函数求最值和二次函数分类讨论问题,注意定义域的问题.

练习册系列答案
相关题目
12.已知f(x)=$\left\{\begin{array}{l}{\frac{-2x+1}{{x}^{2}}\\ x>0}\\{\frac{1}{x}\\ x<0}\end{array}\right.$,则f(x)>-1的解集为( )
| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,-1)∪(0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,0)∪(0,1) |
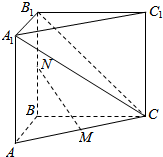 如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.