题目内容
3.把1-9这9个数字排成三列三行的方阵$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{{a}_{13}}\\{{a}_{21}}&{{a}_{22}}&{{a}_{23}}\\{{a}_{31}}&{{a}_{32}}&{{a}_{33}}\end{array})$3×3(1)若偶数只能排在对角线的位置上,共有多少种不同的排法?
(2)在方阵中任取三个数,所取三数中至少有两数位于同行或同列的概率等于多少?
(3)若将其中一个三列三行的方阵中的数按如下要求排到一个一行九列方阵中:①原方阵第一行三个数的前后相对次序不变(即a11要求排在a12的左边,a13安排在a12的右边,但可以不相邻);②第二行的三个数不相邻;③第三行的三个数不相邻且不排在第1和第9的位置,共有多少种不同的变换方法?
分析 (1)先排列偶数2、4、6、8,再排列剩余的数字即可;
(2)求出方阵中任取三个数,其中三个数中任两个不同行不同列的概率,即可得出所求结果;
(3)以方阵中第一行三个数的相对次序为基础,排第二行的三个数,再排第三行的三个数,即可求出结果.
解答 解:(1)当偶数2、4、6、8只能排在对角线的位置上时,
共有${A}_{5}^{4}$•${A}_{5}^{5}$=14400种不同的排法;
(2)在方阵中任取三个数,即从9个数中任选3个,共有${C}_{9}^{3}$=84种不同选法,
其中三个数中任两个不同行不同列的为:
(a11,a22,a33),(a11,a23,a32),
(a12,a21,a33),(a12,a23,a31),
(a13,a22,a31),(a13,a21,a32)共6个,
∴所取三数中至少有两数位于同行或同列的概率为P=1-$\frac{6}{84}$=$\frac{13}{14}$;
(3)根据题意,先以方阵中第一行三个数的前后相对次序不变为基础,
再排列第二行的三个数,有${A}_{4}^{3}$种不同的方法;
最后排列第三行的三个数,有${A}_{5}^{3}$种不同的方法;
所以,总共有${A}_{4}^{3}$•${A}_{5}^{3}$=1440种不同的方法.
点评 本题考查了排列与组合数的应用问题,也考查了古典概率的计算问题,是综合性题目.

练习册系列答案
相关题目
12.已知f(x)=$\left\{\begin{array}{l}{\frac{-2x+1}{{x}^{2}}\\ x>0}\\{\frac{1}{x}\\ x<0}\end{array}\right.$,则f(x)>-1的解集为( )
| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,-1)∪(0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,0)∪(0,1) |
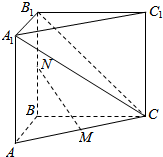 如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.