题目内容
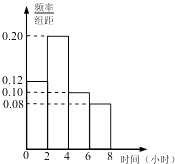
【题目】某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
分组 | 频数 | 频率 |
[60,70] |
| 0.16 |
(70,80] | 22 |
|
(80,90] | 14 | 0.28 |
(90,100] |
|
|
合计 | 50 | 1 |
(Ⅰ)确定表中![]() 的值(直接写出结果,不必写过程)
的值(直接写出结果,不必写过程)
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
![]() 求该选手答完3道题而通过第一关的概率;
求该选手答完3道题而通过第一关的概率;
![]() 记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
【答案】(Ⅰ)![]() (Ⅱ)见解析;
(Ⅱ)见解析; ![]()
【解析】【试题分析】(1)借助频率、频数、样本容量之间的关系![]() 进行求解;(2)先依据题设中答题的要求,运用互斥事件和对立事件的概率计算公式进行分析求解;(3)先求出随机变量
进行求解;(2)先依据题设中答题的要求,运用互斥事件和对立事件的概率计算公式进行分析求解;(3)先求出随机变量![]() 的值进行分类
的值进行分类![]() ,分别求出其概率
,分别求出其概率![]() ,
, ![]() ,
, ![]() ,列出概率分布表,再运用随机变量的数学期望公式计算求解:
,列出概率分布表,再运用随机变量的数学期望公式计算求解:
解:(I)由频率分布表可得a=8,b=6,x=0.44,y=0.12
(II)由频率分布表及(I)的结论可知,该选手能进入面试的概率即答对每道题的概率为0.28+0.12=0.4.记“答对第i道题”为事件Ai,i=1,2,3,4,则P(Ai)=0.4
![]() 记“该选手答完3道题而通过第一关”为事件A,
记“该选手答完3道题而通过第一关”为事件A,
则![]() =0.192
=0.192
![]() 随机变量X的可能取值为2,3,4.
随机变量X的可能取值为2,3,4.
![]()
![]()
![]()
故X的分布列为
X | 2 | 3 | 4 |
P | 0.16 | 0.408 | 0.432 |
所以![]() .
.

练习册系列答案
相关题目