题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的一个长轴顶点为A(2,0),离心率为
=1(a>b>0)的一个长轴顶点为A(2,0),离心率为 ![]() ,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△AMN的面积为 ![]() 时,求k的值.
时,求k的值.
【答案】解:(Ⅰ)∵椭圆一个顶点为A (2,0),离心率为 ![]() ,
,
∴ 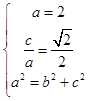
∴b= ![]()
∴椭圆C的方程为 ![]() ;
;
(Ⅱ)直线y=k(x﹣1)与椭圆C联立 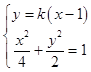 ,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0
,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0
设M(x1 , y1),N(x2 , y2),则x1+x2= ![]() ,
, ![]()
∴|MN|= ![]() =
= 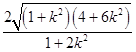
∵A(2,0)到直线y=k(x﹣1)的距离为 ![]()
∴△AMN的面积S= ![]()
∵△AMN的面积为 ![]() ,
,
∴ ![]()
∴k=±1
【解析】(Ⅰ)根据椭圆一个顶点为A (2,0),离心率为 ![]() ,可建立方程组,从而可求椭圆C的方程;(Ⅱ)直线y=k(x﹣1)与椭圆C联立
,可建立方程组,从而可求椭圆C的方程;(Ⅱ)直线y=k(x﹣1)与椭圆C联立 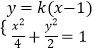 ,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0,从而可求|MN|,A(2,0)到直线y=k(x﹣1)的距离,利用△AMN的面积为
,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0,从而可求|MN|,A(2,0)到直线y=k(x﹣1)的距离,利用△AMN的面积为 ![]() ,可求k的值.
,可求k的值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

【题目】某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
分组 | 频数 | 频率 |
[60,70] |
| 0.16 |
(70,80] | 22 |
|
(80,90] | 14 | 0.28 |
(90,100] |
|
|
合计 | 50 | 1 |
(Ⅰ)确定表中![]() 的值(直接写出结果,不必写过程)
的值(直接写出结果,不必写过程)
(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
![]() 求该选手答完3道题而通过第一关的概率;
求该选手答完3道题而通过第一关的概率;
![]() 记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.

