题目内容
11.设函数f(x)=sin(2x+φ)(0<φ<π)在x=$\frac{π}{2}$处取得最值,若数列{xn}是首项与公差均为$\frac{π}{4}$的等差数列,则f(x1)+f(x2)+f(x3)+…+f(x2015)的值为-1.分析 由条件求得φ=$\frac{π}{2}$,可得 函数f(x)=cos2x.f(x1)+f(x2)+f(x3)+…+f(x2015)=f($\frac{π}{4}$)+f($\frac{2π}{4}$)+f($\frac{3π}{4}$)+…+f($\frac{2015π}{4}$),再利用余弦函数的周期性求得它的值.
解答 解:由题意可得sin(π+φ)=-sinφ=±1,∴φ=kπ+$\frac{π}{2}$,k∈Z.结合0<φ<π,可得φ=$\frac{π}{2}$,
∴函数f(x)=cos2x.
又 xn=$\frac{nπ}{4}$,f(x1)+f(x2)+f(x3)+…+f(x2015)=f($\frac{π}{4}$)+f($\frac{2π}{4}$)+f($\frac{3π}{4}$)+…+f($\frac{2015π}{4}$)
=cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$+cos2π+…+cos($\frac{2015π}{2}$)
=503×(cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$+cos2π )+cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$=503×0+0-1+0=-1,
故答案为:-1.
点评 本题主要考查正弦函数的最值,利用余弦函数的周期性求函数的值,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.下列命题中正确的个数是( )
?①y=sinx的递增区间是[2k$π,2kπ+\frac{π}{2}$]
?②y=sinx是递增函数.
?③y=sinx在$[{-\frac{π}{2},\frac{π}{2}}]$上是增函数.
?①y=sinx的递增区间是[2k$π,2kπ+\frac{π}{2}$]
?②y=sinx是递增函数.
?③y=sinx在$[{-\frac{π}{2},\frac{π}{2}}]$上是增函数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
3.已知等比数列{an}的公比为正数,且a8a2=2a42,a1=1则a2=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
1.已知函数f(x)=x3-px2-qx的图象与x轴切于点(1,0),则f(x)的极值为( )
| A. | 极大值为$\frac{4}{27}$,极小值为0 | B. | 极大值为0,极小值为$\frac{4}{27}$ | ||
| C. | 极小值为-$\frac{4}{27}$,极大值为0 | D. | 极大值为-$\frac{4}{27}$,极小值为0 |
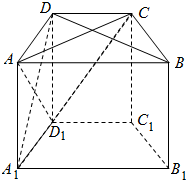
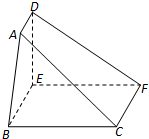 如图,在五面体ABC-DEF中,四边形BCFE是平行四边形.
如图,在五面体ABC-DEF中,四边形BCFE是平行四边形.