题目内容
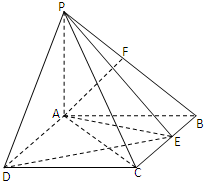
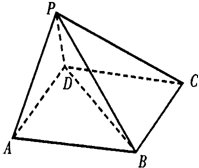
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
,PD=
.
(1)求证:BD⊥平面PAD;
(2)若PD与底面ABCD成60°的角,试求二面角P-BC-A的大小.
| 15 |
| 3 |
(1)求证:BD⊥平面PAD;
(2)若PD与底面ABCD成60°的角,试求二面角P-BC-A的大小.

解(1)由已知AB=4,AD=2,∠BAD=60°,
得BD2=AD2+AB2-2AD•ABcos60°=4+16-2×2×4×
=12.
∴AB2=AD2+BD2,∴△ABD是直角三角形,
∠ADB=90°,即AD⊥BD.
在△PDB中,PD=
,PB=
,BD=
,
∴PB2=PD2+BD2,故得PD⊥BD.
又PD∩AD=D,∴BD⊥平面PAD.
(2)∵BD⊥平面PAD,BD?平面ABCD,
∴平面PAD⊥平面ABCD.
作PE⊥AD于E,又PE?平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°=
•
=
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.
又EF=BD=
,∴在Rt△PEF中,
tan∠PFE=
=
=
.
故二面角P-BC-A的大小为arctan
.
得BD2=AD2+AB2-2AD•ABcos60°=4+16-2×2×4×
| 1 |
| 2 |
∴AB2=AD2+BD2,∴△ABD是直角三角形,
∠ADB=90°,即AD⊥BD.
在△PDB中,PD=
| 3 |
| 15 |
| 12 |
∴PB2=PD2+BD2,故得PD⊥BD.
又PD∩AD=D,∴BD⊥平面PAD.
(2)∵BD⊥平面PAD,BD?平面ABCD,
∴平面PAD⊥平面ABCD.
作PE⊥AD于E,又PE?平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.
又EF=BD=
| 12 |
tan∠PFE=
| PE |
| EF |
| ||
2
|
| ||
| 4 |
故二面角P-BC-A的大小为arctan
| ||
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目