题目内容
17.在△ABC中,角A,B,C的对边边长分别为a,b,c且满足csinA=acosC,则$\sqrt{3}$sinA-cos(B+$\frac{π}{4}$)的最大值为2.分析 由题意和正弦定理可得B=$\frac{3π}{4}$-A,0<A<$\frac{3π}{4}$,进而由三角函数公式可得$\sqrt{3}$sinA-cos(B+$\frac{π}{4}$)=2sin(A+$\frac{π}{6}$),可得最值.
解答 解:∵在△ABC中,角A,B,C的对边边长分别为a,b,c且满足csinA=acosC,
∴由正弦定理可得sinCsinA=sinAcosC,∵sinA≠0,
∴sinC=cosC,∴C=$\frac{π}{4}$,∴B=$\frac{3π}{4}$-A,0<A<$\frac{3π}{4}$,
∴$\sqrt{3}$sinA-cos(B+$\frac{π}{4}$)=$\sqrt{3}$sinA-cos($\frac{3π}{4}$-A+$\frac{π}{4}$)
=$\sqrt{3}$sinA+cosA=2sin(A+$\frac{π}{6}$),
∴当A=$\frac{π}{3}$时,上式取到最大值2
故答案为:2
点评 本题考查三角函数的最值,涉及正弦定理和三角函数公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知一个几何体的三视图如图所示,则该几何体的体积为( )
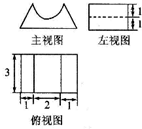

| A. | 27-$\frac{3π}{2}$ | B. | 18-$\frac{3π}{2}$ | C. | 27-3π | D. | 18-3π |
 一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.
一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图. 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).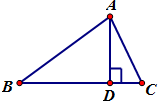 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )