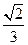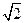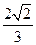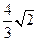题目内容
三棱锥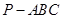 的四个顶点都在体积为
的四个顶点都在体积为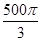 的球的表面上,平面
的球的表面上,平面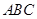 所在的小圆面积为
所在的小圆面积为 ,则该三棱锥的高的最大值是( )
,则该三棱锥的高的最大值是( )
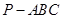 的四个顶点都在体积为
的四个顶点都在体积为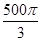 的球的表面上,平面
的球的表面上,平面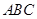 所在的小圆面积为
所在的小圆面积为 ,则该三棱锥的高的最大值是( )
,则该三棱锥的高的最大值是( )| A.7 | B.7.5 | C.8 | D.9 |
C
设球的半径为R,由球的体积公式得: 4/3πR3= 500/3π,∴R=5。
又设小圆半径为r,则πr2=16π,∴r=4.
显然,当三棱锥的高过球心O时,取得最大值;
由OO12= 52-42,得OO1=3,所以高PO1=PO+OO1=5+3=8。
故选C。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
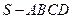 中,底面
中,底面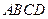 是菱形,
是菱形, ,
,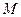 为
为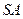 的中点,
的中点,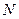 为
为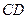 的中点.
的中点.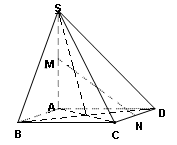
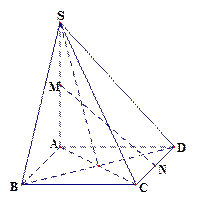
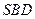
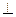 平面
平面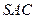 ;
;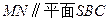 .
.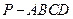 中,底面
中,底面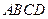 是直角梯形,
是直角梯形,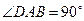 ,
,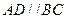 ,
,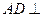 侧面
侧面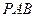 ,△
,△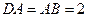 ,
, 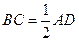 ,
,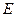 是线段
是线段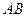 的中点.
的中点.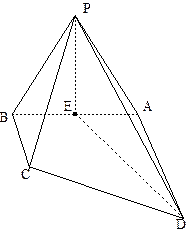
 ;
;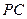 与平面
与平面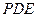 所成角的正弦值.
所成角的正弦值.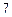 所示的几何体中,
所示的几何体中,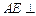 平面
平面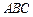 ,
,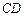 ∥
∥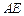 ,
,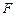 是
是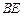 的中点,
的中点,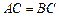
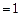 ,
,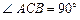 ,
,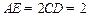 .
.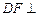 平面
平面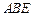 ;
;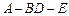 的余弦值.
的余弦值.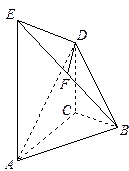
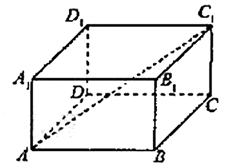
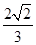
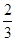
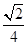
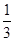
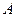 、
、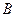 、
、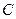 、
、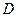 是半径为
是半径为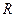 的球面上的四点,且满足
的球面上的四点,且满足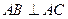 ,
,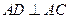 ,
,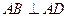 ,则
,则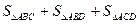 的最大值是 ( )
的最大值是 ( )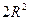
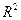
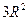
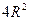
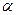 ,
,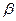 ,
,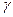 是三个不同平面,给出下列命题:
是三个不同平面,给出下列命题: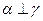 ,
,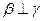 ,则
,则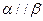 ;
;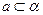 ,
,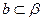 ,
,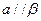 ,
,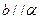 ,则
,则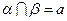 ,
,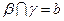 ,
,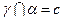 ,且
,且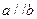 ,则
,则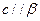 ;
;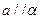 ,
,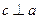 ,
,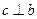 ,则
,则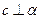 .
.