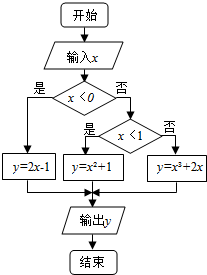
题目内容
13.在比赛中,如果运动员甲胜运动员乙的概率是$\frac{2}{3}$,那么在五次比赛中,运动员甲恰有三次获胜的概率是( )| A. | $\frac{40}{243}$ | B. | $\frac{80}{243}$ | C. | $\frac{110}{243}$ | D. | $\frac{20}{243}$ |
分析 由条件利用n次独立重复实验中恰好发生k次的概率计算公式,计算求得结果.
解答 解:根据每次比赛中,甲胜运动员乙的概率是$\frac{2}{3}$,故在五次比赛中,
运动员甲恰有三次获胜的概率是${C}_{5}^{3}$•${(\frac{2}{3})}^{3}$•${(1-\frac{2}{3})}^{2}$=$\frac{80}{243}$,
故选:B.
点评 本题主要考查n次独立重复实验中恰好发生k次的概率计算公式,属于基础题.

练习册系列答案
相关题目
2.把一段长为12的细铁丝锯成两段,各自围成一个正三角形,那么这两个正三角形的面积之和的最小值是( )
| A. | $2\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | 4 |
3.A={x||x-1|≥1,x∈R},B={x|log2x>1,x∈R},则“x∈A”是“x∈B”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分也非必要条件 |