题目内容
【题目】(13分)
在平面直角坐标系xOy中,抛物线![]() 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足![]() (如图所示).
(如图所示).
(Ⅰ)求![]() 得重心G(即三角形三条中线的交点)的轨迹方程;
得重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
【答案】
解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则 (1)…1分
(1)…1分
∵OA⊥OB ∴![]() ,即
,即![]() ,(2)…………3分
,(2)…………3分
又点A,B在抛物线上,有![]() ,代入(2)化简得
,代入(2)化简得![]() …4分
…4分
∴![]()
所以重心为G的轨迹方程为![]() ……………………………………6分
……………………………………6分
(II)![]()
由(I)得![]() ……11分
……11分
当且仅当![]() 即
即![]() 时,等号成立。………………………12分
时,等号成立。………………………12分
所以△AOB的面积存在最小值,存在时求最小值1; …………………13分

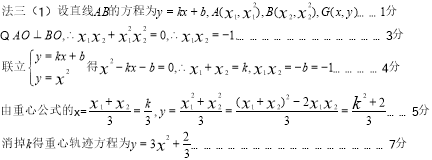

【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: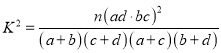 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |