Question

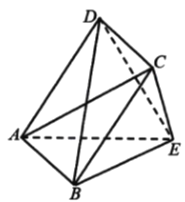
【题目】如图，在三棱柱ABC－A1B1C1中，侧棱垂直于底面，∠BAC＝120°，AC＝AB＝2，AA1＝3．

（1）求三棱柱ABC－A1B1C1的体积；

（2）若M是棱BC的一个靠近点C的三等分点，求证：AM⊥平面ABB1A1．

Answer 1

【答案】（1）（2）详见解析

【解析】

(1)根据体积公式底面积乘以高，代入数据即可；（2）根据余弦定理得到AM=CM,结合等腰三角形底角相等得到AM⊥AB，再由侧楞垂直于底面得到AA1⊥AM，进而得证.

（1）因为∠BAC＝120°，AC＝AB＝2，

所以．

所以．

（2）证明：在△ABC中，由余弦定理，得BC2＝AC2＋AB2－2×AC×AB×cos∠BAC

，

所以．

因为M是棱BC的一个靠近点C的三等分点，

所以．

因为∠BAC＝120°，AC＝AB＝2，

所以∠ACB＝∠ABC＝30°．

由余弦定理，得AM2＝AC2＋CM2－2×AC×CM×cos∠ACB

，

所以．

所以CM＝AM．

所以∠ACM＝∠CAM＝30°．

所以∠MAB＝∠CAB－∠CAM＝120°－30°＝90°．即AM⊥AB．

易知AA1⊥平面ABC，AM平面ABC，

所以AA1⊥AM．

又因为AB∩AA1＝A，所以AM⊥平面ABB1A1．