题目内容
【题目】O为坐标原点,直线l与圆x2+y2=2相切.
(1)若直线l分别与x、y轴正半轴交于A、B两点,求△AOB面积的最小值及面积取得最小值时的直线l的方程.
(2)设直线l交椭圆 ![]() =1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
=1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
【答案】
(1)解:设直线l的方程为 ![]() =1(a,b>0),
=1(a,b>0),
由直线和圆x2+y2=4相切,可得 ![]() =
= ![]() ,
,
即有 ![]() =
= ![]() ≥
≥ ![]() ,即ab≥4,
,即ab≥4,
当且仅当a=b=2时,取得等号.
则△AOB面积S= ![]() ab的最小值为2;
ab的最小值为2;
此时直线的方程为x+y﹣2=0
(2)解:若直线的斜率不存在,设为x=t,
由直线和圆相切可得,t=﹣ ![]() 或
或 ![]() .
.
代入椭圆方程可得,y=± ![]() ,
,
可得中点M坐标为(﹣ ![]() ,0)或(
,0)或( ![]() ,0),|OM|=
,0),|OM|= ![]() ;
;
设直线l的方程为y=kx+m,代入椭圆方程可得,
(1+2k2)x2+4kmx+2m2﹣6=0,
△=16k2m2﹣4(1+2k2)(2m2﹣6)>0,
即为m2<3+6k2,
由直线和圆相切,可得 ![]() =
= ![]() ,
,
即为m2=2+2k2,由2+2k2<3+6k2,可得k∈R,
设P,Q的坐标为(x1,y1),(x2,y2),
可得x1+x2=﹣ ![]() ,中点M的坐标为(﹣
,中点M的坐标为(﹣ ![]() ,
, ![]() ),
),
即有|OM|= ![]() =
= ![]()
设1+2k2=t(t≥1),则|OM|= ![]() =
= ![]()
= ![]() ,由t≥1可得t=2取得最大值
,由t≥1可得t=2取得最大值 ![]() ,
,
t=1时,取得最小值 ![]() .
.
故|OM|的范围是[ ![]() ,
, ![]() ]
]
【解析】(1)设出直线方程,由直线和圆相切的条件:d=r,结合基本不等式,即可得到面积的最小值和此时直线的方程;(2)讨论直线的斜率不存在和存在,设出直线方程为y=kx+m,代入椭圆方程,运用韦达定理和中点坐标公式,结合判别式大于0,化简整理即可得到所求范围.

 阅读快车系列答案
阅读快车系列答案【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() .
.
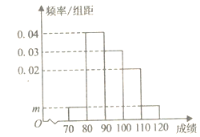
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) |
x:y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |