Question

【题目】已知圆心在轴的正半轴上，且半径为2的圆被直线截得的弦长为.

（1）求圆的方程；

（2）设动直线与圆交于两点，则在轴正半轴上是否存在定点，使得直线与直线关于轴对称？若存在，请求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）（2）当点为时，直线与直线关于轴对称，详见解析

【解析】

（1）设圆的方程为，由垂径定理求得弦长，再由弦长为可求得，从而得圆的方程；

（2）假设存在定点，使得直线与直线关于轴对称，则，同时设，直线方程代入圆方程后用韦达定理得，即为，代入可求得，说明存在．

（1）设圆的方程为：

圆心到直线的距离

根据垂径定理得，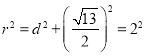

，解得，

，故圆的方程为

（2）假设存在定点，使得直线与直线关于轴对称，

那么，

设

联立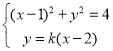得：

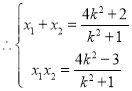
由

.

故存在，当点为时，直线与直线关于轴对称.