题目内容
【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: ![]() .
.
【答案】解:(Ⅰ)不等式f(1)+f(﹣2)≥5等价于|m+1|+|m﹣2|≥5,
可化为  ,解得m≤﹣2;
,解得m≤﹣2;
或 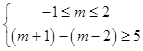 ,无解;
,无解;
或  ,解得m≥3;
,解得m≥3;
综上不等式解集为(﹣∞,﹣2]∪[3,+∞)
(Ⅱ)证明:当x≠0时, ![]() ,|x|>0,
,|x|>0,![]()
【解析】(Ⅰ)问题等价于|m+1|+|m﹣2|≥5,通过讨论m的范围,求出不等式的解集即可;(Ⅱ)根据绝对值的性质证明即可.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

【题目】随着经济的发展,某地最近几年某商品的需求量逐年上升.下表为部分统计数据:
年份 |
|
|
|
|
|
需求量 |
|
|
|
|
|
为了研究计算的方便,工作人员将上表的数据进行了处理,令![]() ,
,![]() .
.
(1)填写下列表格并求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
时间代号 | |||||
|
(2)根据所求的线性回归方程,预测到![]() 年年底,某地对该商品的需求量是多少?
年年底,某地对该商品的需求量是多少?
(附:线性回归方程![]() ,其中
,其中 ,
,![]() )
)
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 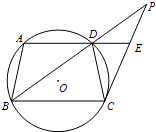
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各![]() 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(Ⅰ)如果抢到红包个数超过![]() 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有![]() 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?
(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的![]() 种型号中各选出
种型号中各选出![]() 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
参考公式:随机变量![]() 的观察值计算公式:
的观察值计算公式:![]() ,
,
其中![]() .临界值表:
.临界值表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |

