题目内容
定义域和值域均为
（常数
）的函数
和
的图像如图所示，给出下列四个命题：
（1）方程
有且仅有三个解；
（2）方程
有且仅有三个解；
（3）方程
有且仅有九个解；
（4）方程
有且仅有一个解。
那么，其中正确命题的个数是 。
（常数）的函数和的图像如图所示，给出下列四个命题：（1）方程
有且仅有三个解；（2）方程
有且仅有三个解；（3）方程
有且仅有九个解；（4）方程
有且仅有一个解。那么，其中正确命题的个数是 。
（1）（4）
考查函数的图像
练习册系列答案
一线名师权威作业本系列答案
相关题目
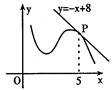
的图象在点P处的切线方程是 
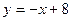，则
= .
的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为
. （Ⅰ）求函数
的解析式；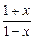
,F(x)=
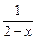+f(x). 
;
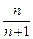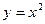到直线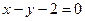
的最短距离为（ ）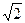
，
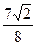
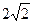
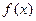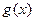是定义在R上的函数，
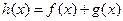，则“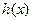
为偶函数”的
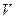的圆柱形水池，已知底的单位面积造价是侧面单位造价的一半，问：如何设计水池的底半径和高，才能使总造价最省？
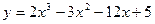在[0，3]上的最大值和最小值分别是_______. 
（位移单位是
，时间单位是
），求物体在
到
时的平均速度及
的平均速度。