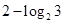题目内容
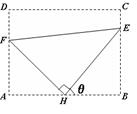
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt∆FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10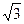 米,记∠BHE=θ.
米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若sinθ+cosθ=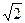 ,求此时管道的长度L;
,求此时管道的长度L;
(3)问:当θ取何值时,污水净化效果最好?
并求出此时管道的长度.
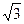 米,记∠BHE=θ.
米,记∠BHE=θ.(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若sinθ+cosθ=
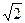 ,求此时管道的长度L;
,求此时管道的长度L;(3)问:当θ取何值时,污水净化效果最好?
并求出此时管道的长度.

解:(1)EH=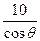 ,FH=
,FH=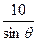 EF=
EF=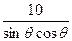 分
分
由于BE=10tanθ≤10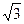 , AF=
, AF= ≤10
≤10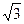 故
故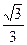 ≤tanθ≤
≤tanθ≤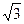 ,θ∈[
,θ∈[ ,
,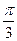 ]分
]分
L=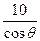 +
+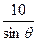 +
+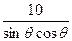 ,θ∈[
,θ∈[ ,
,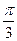 ]
]
(2) sinθ+cosθ=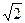 时,sinθ•cosθ=
时,sinθ•cosθ=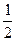 , L=20(
, L=20(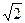 +1);
+1);
(3)L=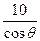 +
+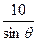 +
+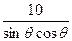 设sinθ+cosθ="t" 则sinθ•cosθ=
设sinθ+cosθ="t" 则sinθ•cosθ=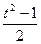
由于θ∈[ ,
,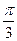 ],所以t=sinθ+cosθ=
],所以t=sinθ+cosθ=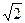
 sin(θ+
sin(θ+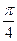 )∈[
)∈[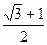 ,
,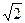 ]
]
L=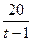 在[
在[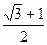 ,
,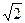 ]内单调递减,
]内单调递减,
于是当t=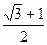 时,即θ=
时,即θ= ,θ=
,θ=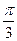 时L的最大值20(
时L的最大值20(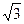 +1)米
+1)米
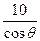 ,FH=
,FH=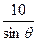 EF=
EF=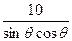 分
分由于BE=10tanθ≤10
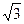 , AF=
, AF= ≤10
≤10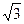 故
故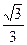 ≤tanθ≤
≤tanθ≤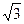 ,θ∈[
,θ∈[ ,
,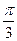 ]分
]分L=
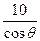 +
+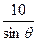 +
+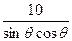 ,θ∈[
,θ∈[ ,
,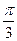 ]
](2) sinθ+cosθ=
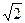 时,sinθ•cosθ=
时,sinθ•cosθ=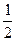 , L=20(
, L=20(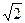 +1);
+1);(3)L=
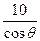 +
+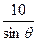 +
+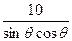 设sinθ+cosθ="t" 则sinθ•cosθ=
设sinθ+cosθ="t" 则sinθ•cosθ=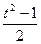
由于θ∈[
 ,
,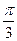 ],所以t=sinθ+cosθ=
],所以t=sinθ+cosθ=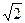
 sin(θ+
sin(θ+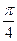 )∈[
)∈[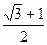 ,
,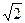 ]
]L=
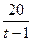 在[
在[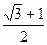 ,
,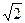 ]内单调递减,
]内单调递减,于是当t=
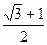 时,即θ=
时,即θ= ,θ=
,θ=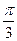 时L的最大值20(
时L的最大值20(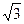 +1)米
+1)米略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 的定义域;
的定义域;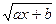 又在其反函数的图象上,求a, b的值
又在其反函数的图象上,求a, b的值 上的奇函数
上的奇函数 满足当
满足当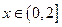 时,
时,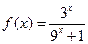 .
.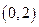 上的单调性,并给予证明;
上的单调性,并给予证明;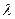 为何值时,关于方程
为何值时,关于方程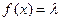 在
在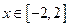 上有实数解?
上有实数解?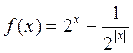
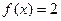 ,求
,求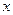 的值;
的值;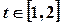 ,
,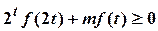 恒成立,求实数
恒成立,求实数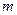 的取值范围。
的取值范围。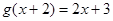 ,则
,则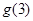 的值是 ( )
的值是 ( )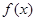 是奇函数,且
是奇函数,且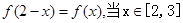 时,
时,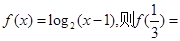 ( )
( )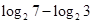 ............
............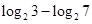
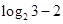 ..........
..........