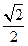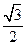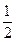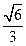��Ŀ����
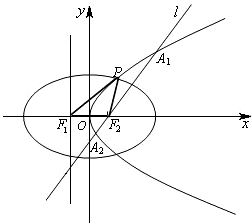
��ͼ����������c1��y2=4mx��m��0��������x�ύ��F1������ΪF2����F1��F2Ϊ���㣬������e=
����Բc2��������c1��x���Ϸ���һ������ΪP��
��1����m=1ʱ������Բ�ķ��̣�
��2���ڣ�1���������£�ֱ��l������Բc2���ҽ���F2����������c1����A1��A2��������߶�A1A2Ϊֱ����Բ�����жϵ�P��Բ��λ�ù�ϵ����˵�����ɣ�
��3���Ƿ����ʵ��m��ʹ�á�PF1F2�ı߳�����������Ȼ���������ڣ����������ʵ��m���������ڣ���˵�����ɣ�
| 1 |
| 2 |
��1����m=1ʱ������Բ�ķ��̣�
��2���ڣ�1���������£�ֱ��l������Բc2���ҽ���F2����������c1����A1��A2��������߶�A1A2Ϊֱ����Բ�����жϵ�P��Բ��λ�ù�ϵ����˵�����ɣ�
��3���Ƿ����ʵ��m��ʹ�á�PF1F2�ı߳�����������Ȼ���������ڣ����������ʵ��m���������ڣ���˵�����ɣ�

��c1��y2=4mx���ҽ���F2��m��0��
����Բ�İ뽹��c=m����e=
��
����Բ�ij�����ij�a=2m���̰���ij�b=
m��
��Բ����Ϊ
+
=1��
��1����m=1ʱ������Բ����Ϊ
+
=1����3�֣�
��2����������ֱ��l�ķ���Ϊ��x=ky+1��k��R
����
�õ�P������ΪP(
��
)��
��x=ky+1����y2=4x��y2-4ky-4=0��
��A1��x1��y1����A2��x2��y2������Τ�ﶨ����y1+y2=4k��y1y2=-4��
��
=(x1-
��y1-
)��
=(x2-
��y2-
)��
•
=x1x2-
(x1+x2)+
+y1y2-
(y1+y2)+
=-
=-
��
��k��R������
•
��ֵ����С���㣬�����㣬�����㣮
����P����Բ�ڣ�Բ�ϻ�Բ�⣮��8�֣�
��3�������������������ʵ��m��
��
��ã�P(
m��
m)��
��|PF2|=
m+m=
m��|PF1|=4m-|PF2|=
m����|F1F2|=2m=
m��
����PF1F2�ı߳��ֱ���
m��
m��
m��
��m=3ʱ����ʹ��PF1F2�ı߳�����������Ȼ������14�֣�

����Բ�İ뽹��c=m����e=
| 1 |
| 2 |
����Բ�ij�����ij�a=2m���̰���ij�b=
| 3 |
��Բ����Ϊ
| x2 |
| 4m2 |
| y2 |
| 3m2 |
��1����m=1ʱ������Բ����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2����������ֱ��l�ķ���Ϊ��x=ky+1��k��R
����
|
| 2 |
| 3 |
2
| ||
| 3 |
��x=ky+1����y2=4x��y2-4ky-4=0��
��A1��x1��y1����A2��x2��y2������Τ�ﶨ����y1+y2=4k��y1y2=-4��
��
| PA1 |
| 2 |
| 3 |
2
| ||
| 3 |
| PA2 |
| 2 |
| 3 |
2
| ||
| 3 |
| PA1 |
| PA2 |
| 2 |
| 3 |
| 4 |
| 9 |
2
| ||
| 3 |
| 24 |
| 9 |
=-
24k2+24
| ||
| 9 |
=-
24(k+
| ||||
| 9 |
��k��R������
| PA1 |
| PA2 |
����P����Բ�ڣ�Բ�ϻ�Բ�⣮��8�֣�
��3�������������������ʵ��m��
��
|
| 2 |
| 3 |
2
| ||
| 3 |
��|PF2|=
| 2 |
| 3 |
| 5 |
| 3 |
| 7 |
| 3 |
| 6 |
| 3 |
����PF1F2�ı߳��ֱ���
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
��m=3ʱ����ʹ��PF1F2�ı߳�����������Ȼ������14�֣�


��ϰ��ϵ�д�
�����Ŀ
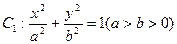 ��������Ϊ
��������Ϊ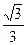 ��ֱ��l��y=x+2����ԭ��ΪԲ�ġ���ԲC1�Ķ̰��᳤Ϊ�뾶��ԲO���У���1������ԲC1�ķ��̣���2������ԲC1����ΪF1���ҽ���ΪF2��ֱ��l1����F1���Ҵ�ֱ����Բ�ij��ᣬ��ֱ��l2��ֱ��l1������Ϊ��P���߶�PF2�Ĵ�ֱƽ���߽�l2�ڵ�M�����M�Ĺ켣C2�ķ��̣���3������ԲC1����A��ֱ��m����ԲO�ཻ������R��S����
��ֱ��l��y=x+2����ԭ��ΪԲ�ġ���ԲC1�Ķ̰��᳤Ϊ�뾶��ԲO���У���1������ԲC1�ķ��̣���2������ԲC1����ΪF1���ҽ���ΪF2��ֱ��l1����F1���Ҵ�ֱ����Բ�ij��ᣬ��ֱ��l2��ֱ��l1������Ϊ��P���߶�PF2�Ĵ�ֱƽ���߽�l2�ڵ�M�����M�Ĺ켣C2�ķ��̣���3������ԲC1����A��ֱ��m����ԲO�ཻ������R��S����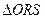 �Ƕ۽������Σ���ֱ��m��б��k��ȡֵ��Χ��
�Ƕ۽������Σ���ֱ��m��б��k��ȡֵ��Χ��
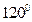 �������Բ��������
�������Բ�������� Ϊ�� ��
�� ��