题目内容

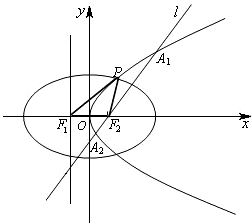
设椭圆C：
x2
a2
+
y2
2
=1(a＞0)的左右焦点分别为F1、F2，A是椭圆C上的一点，且
AF2
•
F1F2
=0，坐标原点O到直线AF1的距离为
1
3
|OF1|．
（1）求椭圆C的方程；
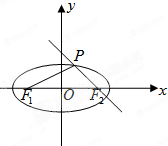
（2）设Q是椭圆C上的一点，过点Q的直线l交x轴于点F（-1，0），交y轴于点M，若|MQ|=2|QF|，求直线l的斜率．
（1）由题设知F1（-
a2-2
，0），F2（
a2-2
，0），其中a＞
2

由于
AF2
•
F1F2
=0，则有
AF2
⊥
F1F2
，所以点A的坐标为（
a2-2
，±
2
a
）
故AF1所在直线方程为y=±（
x
a
a2-2
+
1
a
），所以坐标原点O到直线AF1的距离为
a2-2
a2-1
，
又|OF1|=
a2-2
，所以
a2-2
a2-1
=|=
1
3
a2-2
，解得：a=2．
∴所求椭圆的方程为
x2
4
+
y2
2
=1．
（2）由题意可知直线l的斜率存在，设直线斜率为k，则直线l的方程为y=k（x+1），故M（0，k）．
设Q（x1，y1），由于Q，F，三点共线，且|MQ|=|2QF|．
根据题意得（x1，y1-k）=±2（x1+1，y1），解得
x1=-2
y1=-k
或
x1=-
2
3
y1=
k
3

又Q在椭圆C上，故
4
4
+
k2
2
=1或
4
9
4
+
(
k
3
)2
3
=1，
解得k=0，k=±4，综上，直线的斜率为0或±4
练习册系列答案
相关题目
如图，设抛物线c1：y2=4mx（m＞0）的准线与x轴交于F1，焦点为F2，以F1、F2为焦点，离心率e=
1
2
的椭圆c2与抛物线c1在x轴上方的一个交点为P．
（1）当m=1时，求椭圆的方程；
（2）在（1）的条件下，直线l经过椭圆c2的右焦点F2，与抛物线c1交于A1、A2，如果以线段A1A2为直径作圆，试判断点P与圆的位置关系，并说明理由；
（3）是否存在实数m，使得△PF1F2的边长是连续的自然数，若存在，求出这样的实数m；若不存在，请说明理由．
若椭圆
x2
m
+
y2
3
=1的右焦点与抛物线y2=12x的焦点重合，则m=（　　）
A．3B．6C．9D．12
已知△ABC的周长是16，A（-3，0），B（3，0），则动点C的轨迹方程是（　　）
A．
x2
25
+
y2
16
=1		B．
x2
25
+
y2
16
=1(y≠0)
C．
x2
16
+
y2
25
=1		D．
x2
16
+
y2
25
=1(y≠0)
点P(2cosα，
3
sinα)（α∈R）与椭圆C：
x2
4
+
y2
3
=1的位置关系是（　　）
A．点P在椭圆C上
B．点P与椭圆C的位置关系不能确定，与α的取值有关
C．点P在椭圆C内
D．点P在椭圆C外
已知椭圆过点（3，0）且离心率为
6
3
，则椭圆标准方程为______．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，若△AF1F2为正三角形且周长为6；
（1）求椭圆C的标准方程；
（2）若椭圆C上存在A，B两点关于直线y=x+m对称，求实数m的取值范围；
（3）若直线l：y=kx+n与椭圆C交于A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证直线l过定点，并求出定点坐标．
已知点P在椭圆
x2
49
+
y2
24
=1上，F1、F2是椭圆的焦点，且PF1⊥PF2，求
（1）|PF1|•|PF2|
（2）△PF1F2的面积．
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个顶点到其左、右两个焦点F1，F2的距离分别为5和1；点P是椭圆上一点，且在x轴上方，直线PF2的斜率为-
15
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）求△F1PF2的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网