题目内容
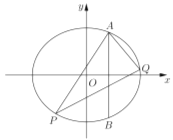
【题目】已知圆![]() 过定点
过定点![]() ,圆心
,圆心![]() 在抛物线
在抛物线![]() 上,
上,![]() 、
、![]() 为圆
为圆![]() 与
与![]() 轴的交点.
轴的交点.
(1)求圆![]() 半径的最小值;
半径的最小值;
(2)当圆心![]() 在抛物线上运动时,
在抛物线上运动时,![]() 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心![]() 在抛物线上运动时,记
在抛物线上运动时,记![]() ,
,![]() ,求
,求![]() 的最大值,并求此时圆的方程.
的最大值,并求此时圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() ,
,![]()
【解析】
(1)设半径为![]() ,根据抛物线方程设出圆心坐标,然后根据圆心和定点写出半径
,根据抛物线方程设出圆心坐标,然后根据圆心和定点写出半径![]() 的表达式,计算
的表达式,计算![]() 的最小值即可;
的最小值即可;
(2)根据(1)中的![]() 表示,写出圆的方程,令
表示,写出圆的方程,令![]() 计算出
计算出![]() 的横坐标,计算
的横坐标,计算![]() 是否为定值即可证明;
是否为定值即可证明;
(3)计算出![]() 的值,然后利用已求的值对
的值,然后利用已求的值对![]() 进行化简,再根据基本不等式确定最大值,从而求出圆心坐标和半径确定出圆的方程.
进行化简,再根据基本不等式确定最大值,从而求出圆心坐标和半径确定出圆的方程.
(1)设圆心坐标为![]() ,半径为
,半径为![]() ,所以
,所以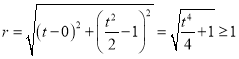 ,取等号时
,取等号时![]() ,所以
,所以![]() ;
;
(2)因为圆心坐标为![]() ,半径
,半径 ,所以圆的方程为:
,所以圆的方程为: ,
,
令![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 为定值
为定值![]() ;
;
(3)由(2)可知:取![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以
 ,
,
所以![]() 的最大值为
的最大值为![]() ,
,
取等号时![]() ,所以
,所以![]() ,所以圆心坐标为
,所以圆心坐标为![]() ,半径
,半径![]() ,
,
所以圆的方程为:![]() .
.

练习册系列答案
相关题目