题目内容
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 、
、![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() ,证明:
,证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() (
(![]() )的
)的![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)1或2.
;(2)证明见解析;(3)1或2.
【解析】
(1)运用数列的递推式和等差数列的定义和通项公式,即可得到所求;
(2)设数列{bn}的公差为d,求出Sn,Tn.由恒成立思想可得b1<1,求出an﹣bn,判断符号即可得证;
(3)运用等差数列和等比数列的求和公式,求得Sn,Tn,化简![]() ,推出小于3,结合等差数列的通项公式和数列的单调性,即可得到所求值.
,推出小于3,结合等差数列的通项公式和数列的单调性,即可得到所求值.
(1)由3Sn+1=2Sn+Sn+2+an,得2(Sn+1﹣Sn)=Sn+2﹣Sn+1+an,
即2an+1=an+2+an,所以an+2﹣an+1=an+1﹣an.
由a1=1,S2=4,可知a2=3.
所以数列{an}是以1为首项,2为公差的等差数列.
故{an}的通项公式为an=1+2(n﹣1)=2n﹣1,n∈N*.
(2)设数列{bn}的公差为d,
则Tn=nb1![]() n(n﹣1)d,
n(n﹣1)d,
由(1)知,Sn![]() n(1+2n﹣1)=n2.
n(1+2n﹣1)=n2.
因为Sn>Tn,所以n2>nb1![]() n(n﹣1)d,
n(n﹣1)d,
即(2﹣d)n+d﹣2b1>0恒成立,
所以 ,即
,即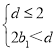 ,
,
又由S1>T1,得b1<1,
所以an﹣bn=2n﹣1﹣b1﹣(n﹣1)d=(2﹣d)n+d﹣1﹣b1≥2﹣d+d﹣1﹣b1=1﹣b1>0.
所以an>bn,得证.
(3)由(1)知,Sn=n2.因为{bn}为等比数列,
且b1=1,b2=3,
所以{bn}是以1为首项,3为公比的等比数列.
所以bn=3n﹣1,Tn![]() (3n﹣1).
(3n﹣1).
则![]() 3
3![]() ,
,
因为n∈N*,所以6n2﹣2n+2>0,所以![]() 3.
3.
而ak=2k﹣1,所以![]() 1,即3n﹣1﹣n2+n﹣1=0(*).
1,即3n﹣1﹣n2+n﹣1=0(*).
当n=1,2时,(*)式成立;
当n≥2时,设f(n)=3n﹣1﹣n2+n﹣1,
则f(n+1)﹣f(n)=3n﹣(n+1)2+n﹣(3n﹣1﹣n2+n﹣1)=2(3n﹣1﹣n)>0,
所以0=f(2)<f(3)<…<f(n)<…,
故满足条件的n的值为1和2.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案