题目内容
【题目】如图,两条相交线段![]() 、
、![]() 的四个端点都在椭圆
的四个端点都在椭圆![]() 上,其中直线
上,其中直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.

(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)探究:是否存在常数![]() ,当
,当![]() 变化时,恒有
变化时,恒有![]() ?
?
【答案】(1)![]() ;(2)存在
;(2)存在![]() ,见解析
,见解析
【解析】
(1)当![]() 时,联立方程组求得
时,联立方程组求得![]() ,根据
,根据![]() ,利用
,利用![]() ,列出方程,即可求解;
,列出方程,即可求解;
(2)设![]() ,由
,由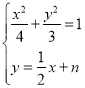 ,得
,得![]() ,利用韦达定理,结合椭圆的对称性,分类讨论,即可得到结论.
,利用韦达定理,结合椭圆的对称性,分类讨论,即可得到结论.
(1)由题意,当![]() 时,联立方程组
时,联立方程组 ,解得
,解得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则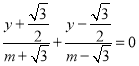 ,化简得
,化简得![]() ,
,
又由![]() ,联立方程组
,联立方程组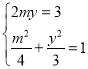 ,解得
,解得![]() 或
或![]() .
.
因为![]() 平分
平分![]() ,所以
,所以![]() (不适合题意),所以
(不适合题意),所以![]() .
.
(2)设![]() ,
,
由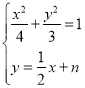 ,整理得
,整理得![]() ,
,
其中![]() ,
,
若存在常数![]() ,当
,当![]() 变化时,恒有
变化时,恒有![]() ,
,
则由(1)可知只可能是![]() ,
,
①当![]() 时,取
时,取![]() ,
,![]() 等价于
等价于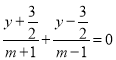 ,
,
即![]() ,
,
即![]() ,
,
即![]() ,此式子恒成立,
,此式子恒成立,
所以存在常数![]() ,当
,当![]() 变化时,恒有
变化时,恒有![]() ;
;
②当![]() 时,取
时,取![]() ,由椭圆的对称性,同理可知结论也成立,
,由椭圆的对称性,同理可知结论也成立,
综上可得,存在常数![]() ,当
,当![]() 变化时,恒有
变化时,恒有![]() ;
;

练习册系列答案
相关题目