题目内容
【题目】已知函数f(x)=x2﹣2(a﹣2)x﹣b2+13.
(1)先后两次抛掷一枚质地均匀的骰子(骰子六个面上分别标有数字1,2,3,4,5,6),骰子向上的数字一次记为a,b,求方程f(x)=0有两个不等正根的概率;
(2)如果a∈[2,6],求函数f(x)在区间[2,3]上是单调函数的概率.
【答案】
(1)解:如果先后抛掷的一枚均匀的骰子所得的向上的点数记为(a,b),
则基本事件总数n=6×6=36,
设事件A表示“f(x)=x2﹣2(a﹣2)x﹣b2+13=0有两个不等正根“,
则事件A满足: 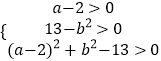 ,
,
满足事件A的基本事件有:(5,3),(6,1),(6,2),(6,3),共有m=4个,
∴方程f(x)=0有两个不等正根的概率p(A)= ![]() .
.
(2)解:设事件B表示“函数f(x)在区间[2,3]上是单调函数”,
∵a∈[2,6],f(x)=x2﹣2(a﹣2)x﹣b2+13的对称轴为x=a﹣2∈[0,4],区间长为4,
f(x)在区间[2,3]上为增函数时,只要对称轴不在[2,3]上即可,
∴对称轴不在[2,3]的区间长为3,
根据几何概型定义得函数f(x)在区间[2,3]上是单调函数的概率P(B)= ![]()
【解析】1、由题意可得基本事件总数=36根据题意二次函数有两个不等的正根利用列举法求出满足事件A的基本事件个数由此求出方程f(x)=0有两个不等正根的概率。
2、由题意可知设事件B表示“函数f(x)在区间[2,3]上是单调函数”根据题意可知f(x)在区间[2,3]上为增函数时只要对称轴不在[2,3]上即可根据几何概型定义得函数f(x)在区间[2,3]上是单调函数的概率。

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:
气温(℃) | 17 | 14 | 11 | ﹣2 |
用电量(度) | 23 | 35 | 39 | 63 |
由表中数据得到线性回归方程 ![]() =﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
=﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
A.38度
B.50度
C.70度
D.30度
【题目】一个生物研究性学习小组,为了研究平均气温与一天内某豆类胚芽生长之间的关系,他们分别记录了4月6日至4月11日的平均气温x(℃)与该豆类胚芽一天生长的长度y(mm),得到如下数据:
日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
该小组的研究方案是:先从这六组数据中选取6日和11日的两组数据作为检验数据,用剩下的4组数据即:7日至10日的四组数据求出线性回归方程.
(1)请按研究方案求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)用6日和11日的两组数据作为检验数据,并判断该小组所得线性回归方程是否理想.(若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm,则认为该方程是理想的)
参考公式:  .
.