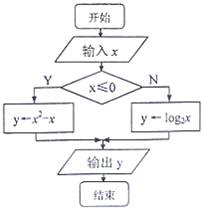
题目内容
2.若{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,则下列各组中不能构成空间一个基底的是( )| A. | $\overrightarrow{a}$,2$\overrightarrow{b}$,3$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$$+\overrightarrow{c}$,$\overrightarrow{c}$$+\overrightarrow{a}$ | C. | $\overrightarrow{a}$+2$\overrightarrow{b}$,2$\overrightarrow{b}$+3$\overrightarrow{c}$,3$\overrightarrow{a}$-9$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{b}$,$\overrightarrow{c}$ |
分析 根据空间向量的共面定理,一组不共面的向量构成空间的一个基底,对选项中的向量进行判断即可.
解答 解:对于A中$\overrightarrow{a}$、2$\overrightarrow{b}$、3$\overrightarrow{c}$,
B中$\overrightarrow{a}$+$\overrightarrow{b}$、$\overrightarrow{b}$+$\overrightarrow{c}$、$\overrightarrow{c}$+$\overrightarrow{a}$,
D中$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$、$\overrightarrow{b}$、$\overrightarrow{c}$,每组都是不共面的向量,能构成空间的一个基底;
对于C,$\overrightarrow{a}$+2$\overrightarrow{b}$、2$\overrightarrow{b}$+3$\overrightarrow{c}$、3$\overrightarrow{a}$-9$\overrightarrow{c}$,
满足3$\overrightarrow{a}$-9$\overrightarrow{c}$=3[($\overrightarrow{a}$+2$\overrightarrow{b}$)-(2$\overrightarrow{b}$+3$\overrightarrow{c}$)],是共面向量,不能构成空间的一个基底.
故选:C.
点评 本题考查了空间向量共面的判断与应用问题,是基础题目.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
12.在△ABC中,若$\overrightarrow{AB}$•$\overrightarrow{BC}$>0,则角B的取值范围是( )
| A. | [$\frac{π}{2}$,π) | B. | ($\frac{π}{2}$,π) | C. | (0,$\frac{π}{2}$] | D. | (0,$\frac{π}{2}$) |
12.如图所示,在三棱台A′B′C′-ABC中,沿A′BC截去三棱锥A′-ABC,则剩余的部分是( )
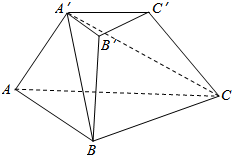

| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 组合体 |